
מאמר מס' 15 בסדרה
פורסם: 2.1.18 צילום, יח"צ;
למען גילוי נאות הכותבים הינם מעריכי שווי ואקטוארים העורכים חוות דעת אקטואריות וכלכליות, נותנים ייעוץ בתחומי הערכות השווי של תאגידים, נכסים בלתי מוחשיים ומכשירים פיננסיים מורכבים וכן מתמנים ע"י בתי משפט ובתי דין כאקטוארים וכמעריכי שווי מוסמכים. הנושאים בהם עוסקים הכותבים בתחום הערכות שווי מימון תאגידי הינם, בין היתר: הערכת שווי תאגידים, מגזרים ויחסי מיזוג; הערכות שווי נכסים בלתי מוחשיים לפי 38 IAS; ייחוס עודף עלות הרכישה (PPA- Purchase Price Allocation) לפי 3 IFRS; בדיקות פגימה (Impairment) למוניטין לפי 36 IAS; הערכת שווי אופציות משובצות, אופציות ריאליות, ערבויות והלוואות לפי 39 IAS; הערכת שווי כלכלי של כתבי אופציות לעובדים (ESOP) לפי 2 IFRS לרבות כלל ה- 409A של ה- IRS; פיצול רכיבי אקוויטי ומכשירי הון/ התחייבות מורכבים (PWERM / CVM / OPM) לפי 32 IAS; הערכת שווי התחייבויות למדען הראשי לפי 20 IAS; קביעת שווי הוגן למחירי העברה בין חברתיים ובין לאומיים (At Arm’s Length) וכיוצא באלה הערכות שווי מימון תאגידי.
- מהן אופציות פריזאיות?
על מנת להסביר לקורא מהן אופציות פריזאיות, עליי להכיר תחילה לקורא שכבר מכיר את ההבדלים שבין אופציות אירופאיות לאופציות אמריקאיות, עוד שלושה סוגים של אופציות.
הסוג הראשון נקרא אופציות "המסתכלות אחורה" (Lookback Options). אופציות "המסתכלות אחורה", המכונות גם אופציות בראיה לאחור (Hindsight Options), הינן סוג של אופציות תלויות-מסלול (Path-Dependent) שבהן התזרים הסופי (payoff) תלוי במחיר המקסימלי או במחיר המינימלי של נכס הבסיס במהלך חיי האופציה. המורכבות שנלווית לחישוב מסוג זה הינה שלאופציה "המסתכלת לאחור" לא קיים מחיר מימוש ידוע וקבוע ולמעשה מחיר המימוש של אופציה "המסתכלת לאחור" נקבע כחלק מתהליך החישוב ולא כנתון. נאמר מראש, לבעיית אופציות על מחיר מקסימלי או מינימלי בראיה לאחור – מה שאומר שעל מנת לאמוד את ערכן הכלכלי יש לעשות שימוש בשיטת הסימולציה של מונטה קרלו.
הסוג השני נקרא אופציות אסייתיות (Asian Options). אופציות אסייתיות הינן מקרה פרטי של אופציות "המסתכלות אחורה", שבהן (באופציות אסייתיות כמובן) התזרים הסופי (payoff) תלוי במחיר הממוצע של נכס הבסיס במהלך חיי האופציה. פעם נוספת, המורכבות שנלווית לחישוב מסוג זה הינה שלאופציה אסייתית לא קיים מחיר מימוש ידוע וקבוע ולמעשה מחיר המימוש של אופציה אסייתית נקבע כחלק מתהליך החישוב ולא כנתון. נאמר מראש, לבעיית אופציות אסייתיות – מה שאומר שעל מנת לאמוד את ערכן הכלכלי יש לעשות שימוש בשיטת הסימולציה של מונטה קרלו.
הסוג השלישי נקרא אופציות חסם (Barrier options). אופציות חסם הינן אופציות תלויות-מסלול, המגיעות בטעמים ובצורות שונים, אולם המאפיין העיקרי שלהן הוא שאופציות אלו 'מופעלות' (Initiated) או 'מתחסלות' (Exterminated) כאשר מחיר נכס הבסיס נוגע בחסם מסוים; כלומר, או שהן נכנסות לתוקף (Knocked In) או שהן יוצאות מתוקף (Knocked Out). למרות שישנם פתרונות בצורת קירובים מתמטיים, טובים יותר או טובים פחות, לבעיית אופציית חסם הרי שעל מנת לאמוד את ערכן הכלכלי יש לעשות שימוש בשיטת הסימולציה של מונטה קרלו.
אופציות פריזאיות (Parisian Options) הינן למעשה הכלאה בין אופציות חסם ואופציות אסייתיות. אופציות פריזאיות הינן אופציות אשר נכנסות לתוקף או יוצאות מתוקף בתנאי שמחיר נכס הבסיס במשך תקופת זמן מוגדרת לא יורד מתחת לחסם מסוים או לא עולה מעל לחסם מסוים. המורכבות שנלווית לחישוב מסוג זה הינה שהוא מתחלק לשני חלקים: החלק הראשון עוסק בחישוב ההסתברות לעמוד בתנאי הכניסה לתוקף או בתנאי היציאה מתוקף של האופציה, בעוד שהחלק השני עוסק בחישוב ערכה הכלכלי של האופציה בתנאי שהאופציה נכנסה לתוקף או יצאה מתוקף עד למועד המבוקש ולבסוף, את התוצאה המתקבלת מהחלק השני של החישוב, אנו מכפילים בהסתברות להגעה לתנאי הכניסה לתוקף או לתנאי היציאה מתוקף. מאחר ואין פתרון אנליטי לבעיית אופציה פריזאית הרי שלצורך חישוב ערכה הכלכלי יש להשתמש בפתרון נומרי כגון שיטות נומריות מהסוג המכונה Finite Difference Method ושיטת סימולציית מונטה-קרלו.
- סימולציית מונטה קרלו
סימולציית "מונטה קרלו" הינה טכניקה מתמטית, המסייעת בקבלת החלטה בתנאי אי וודאות שמשלבת שימוש במספרים אקראיים, בהתפלגויות ערכים אפשריות ובהסתברויות, ומסייעת בפתרון בעיות הקשורות לניהול סיכונים ותחזיות לעתיד. הטכניקה מבוססת על בניית מודל נתונים המתאר את הבעיה הכלכלית הניצבת בפני מקבלי ההחלטות. המודל מכיל בדרך כלל משתני כניסה, חישובים ועיבודים שונים הנעשים על משתני הכניסה ותוצאות או תחזיות המשמשות כתוצאות של המודל. מכיוון שאנו פועלים בסביבה שבה חלק ממשתני הכניסה אינם ידועים, וקיימת חוסר ודאות לגביהם, אנו מגדירים עבור אותם משתנים טווחים אפשריים והתפלגויות חזויות לערכים המספריים. הערך המוסף העיקרי של "סימולציית מונטה קרלו" הוא שהיא מציגה עבור משתני התחזית של המודל לא רק את ערכי התוצאה החזויים כמו בניתוחי רגישות וכלים מתמטיים וסטטיסטיים אחרים, אלא גם מהי ההסתברות שיתקבלו אותם ערכים חזויים. ובכך, הסימולציה מצמצמת באופן ניכר את חוסר הודאות של מקבל ההחלטה
טכניקה מדעית זו נמצאת בשימוש רחב בעולם הפיננסים וההשקעות, בהנדסה, ביולוגיה חישובית, כימיה וסטטיסטיקה יישומית ומהווה כלי עזר חשוב בקבלת החלטות.
כהערה אינפורמטיבית נציין כי אנו משתמשים בסימולציית מונטה קרלו גם במסגרת הערכת שווי חברה או פעילות עסקית לצורך בחינת תוצאות עבודתנו המתקבלות ממודל ה- DCF באמצעות שימוש במודלMonte Carlo, המבוסס סדרות סימולציית משתני החלטה סטטיסטיים סטוכסטיים (1,000 איטרציות) המבוססים על סטיות תקן ותוחלת משתני החלטה (Variable Factors) קריטיים במודל Monte Carlo, על ידי חישוב איטרטיבי לשווי אקוויטי החברה למצבי טבע ותרחישים שונים. מודל Monte Carlo משמש לשם בחינת התפלגות התוצאות ביחס לשונות ותוחלת משתנים פרוספקטיביים קריטיים לתוצאות הערכת השווי וביחס לתוצאות פעילות רטרוספקטיביות של החברה. המשתנים הקריטיים שאנו בוחנים הינם שונות ותוחלת משתני ה- WACC, שיעורי צמיחת הכנסות החברה על פני אופק ההיוון, שיעור הצמיחה הפרמננטי בטווח הארוך (Perpetuity), שולי ההוצאות השונים ושיעורי ההשקעות השונים הקשורים לפעילות המוערכת.
להלן דוגמא לפלט סימולציית מונטה קרלו שנבנה במשרד הייעוץ "שווי פנימי".
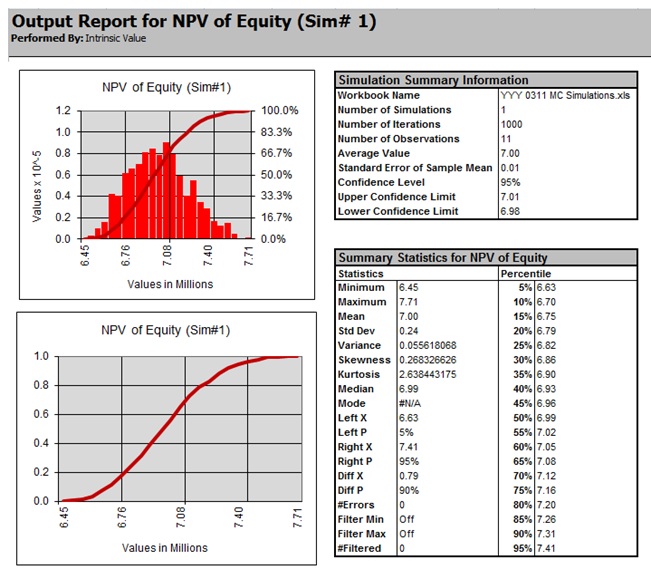
נסביר כי מניתוח הפלט לעיל עולה כי שווי ההון העצמי של החברה בטווח סטיית תקן אחת, נאמד בטווח של כ- 6.76-7.24 מיליון שקלים חדשים (בתוחלת כ- 7.0 מיליון שקלים חדשים), בעיקר בשל התנודתיות הגבוהה בשיעורי צמיחת הכנסות החברה הן הפרוספקטיביות והן הרטרוספקטיביות, המצביעה על הסיכונים הגלומים בפעילותה, אשר נבחנה יחד עם משתנים קריטיים נוספים לחישוב שווי אקוויטי החברה, כאמור לעיל. טווח שווי ההון העצמי של החברה עולה בקנה אחד עם מתודת ה- DCF אשר שימשה בעבודה.
נחזור לסימולציית מונטה קרלו. ניתן ליישם את סימולציה מונטה-קרלו בתחומים שונים, במיוחד כאשר מנסים למדל את התנהגותן של מערכות, הכוללות בחובן מידה מסוימת של אי ודאות. למשל כאשר, המטרה היא למדל את התנהגותו של מחיר נכס בסיס כלשהו על ידי יצירת מסלולי מחירים אפשריים רבים. על מנת לתרחש את המסלולים הללו, עלינו להניח תחילה הנחה כלשהי לגבי התהליך הסטוכסטי השולט במחיר הנכס – במקרה של נכסים פיננסיים, מקובל להניח תנועה בראון גאומטרית (GBM- Geometric Brownian Motion).
תנועה בראון גיאומטרית היא שמו של התהליך הסטוכסטי העומד מאחורי תנועת התנהגות מחיריהם של נכסים פיננסיים. תנועה בראון גיאומטרית גורסת כי מחירים הינם בעלי תנודתיות מתמדת המורכבת משינויים אקראיים ("הילוך מקרי" Random walk), בתוספת "סחיפה" Drift, משמע, שמחיריהם של מטבעות, ריביות, מדדים, ניירות ערך וסחורות אינם נשארים אף פעם במקום אלא הם נעים ונדים כל הזמן על פני מגמה מסוימת תוך זעזועי שוק אקראיים כאלה ואחרים, המסיטים אותם כל פעם מחדש מהתקדמותם על פני אותה סחיפה.

למרות שסימולציית מונטה-קרלו שימושית יותר ככל שמספר המימדים בבעיית הערכת השווי גדול יותר – על ידי זה שהיא מקטינה את הצורך בפתרון משוואות הפרשים רב-מימדיות כמובן – הרי שהשימוש בה לצורך הערכת שווי אופציות אירופאיות (קרי, פשוטות יחסית) הוא די שכיח.
יש לציין כי המספר המקרי הנורמלי הסטנדרטי המשמש ברוב המקרים בסימולציית מונטה קרלו הינו למעשה מספר 'פסאודו-מקרי' (Pseudo Random, כלומר מספר שמתיימר להיות מקרי אך לא באמת כזה), למרות שבמרבית המקרים השימוש במספר פסאודו-מקרי איננו משפיע על הערכת שווי האופציה באופן משמעותי. היות וחלק ממעריכי השווי בוחרים להשתמש במספרים קוואזי 'מקריים' הרי שכאן נכנסת לתמונה סימולציית קוואזי-מונטה-קרלו (Quasi-Monte Carlo Simulation).
- סימולציית קוואזי-מונטה-קרלו (רצפי התאמה נמוכה)
כפי ששמה מרמז סימולציית קוואזי-מונטה-קרלו הינה וריאציה של שיטת סימולציית מונטה-קרלו להערכת שווי אופציות. בעוד ששיטת סימולציית מונטה-קרלו משתמשת במספרים פסאודו-מקריים, הרי שסימולציית קוואזי-מונטה-קרלו משתמשת ברצפי התאמה נמוכה (low discrepancy sequences). ניתן להמחיש זאת כקופסא המלאה בנקודות המסודרות בסדר פסאודו-מקרי; למרות שנקודות אלו ממלאות את התיבה לכאורה באופן מקרי, הרי שבשל תכונותיהן האינהרנטיות נוכל לראות בבירור קיבוצים (Groupings) של נקודות ולא בלאגן אשר מעיד על אקראיות.
באמצעות רצפי התאמה נמוכה ולמרות ש'מקריות' אמיתית לא נוצרה, ניתן לקבל מספרים הקרובים מספיק למספרים מקריים ויכולים לשמש בשיטות מונטה קרלו. ישנם מספר רצפי התאמה נמוכה אשר ניתן להשתמש בהם בסימולציית קוואזי-מונטה-קרלו:
- Faure
- Halton
- Sobol
- Niederreiter
- Van der Corput
- דוגמא להערכת שווי כלכלי של כתבי אופציות פריזאיות על בסיס Barrier Flexible Monte-Carlo Model
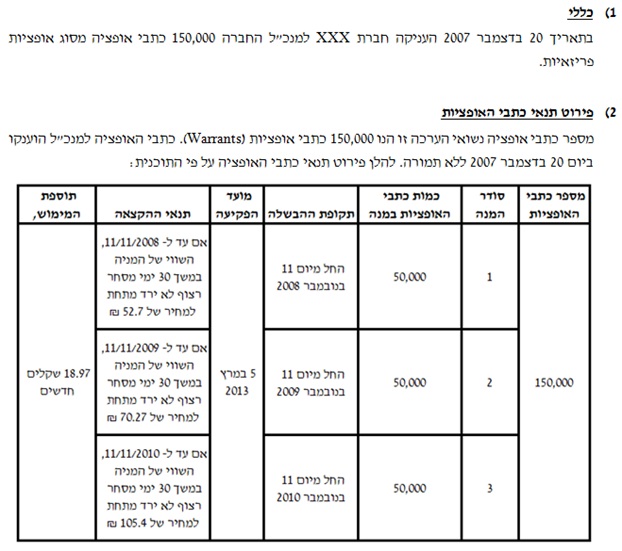



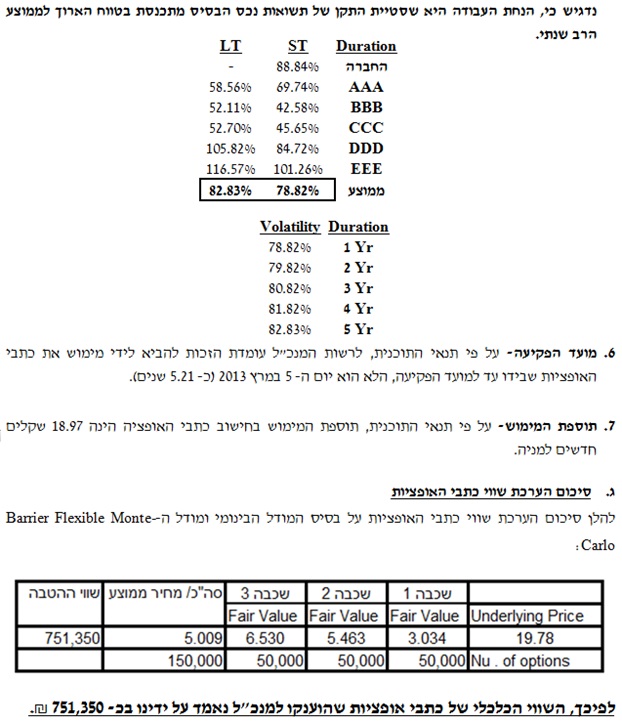
המשך במאמר הבא….

הכותב יוסי דקל הינו הבעלים של משרד הייעוץ הכלכלי K.O. Dekel & Co., במתן ייעוץ כלכלי, חוות דעת מומחה כלכליות ואקטואריות והערכות שווי מקצועיות בלתי תלויות, מרצה בתחומים כלכליים שונים, חבר מערכת בכתב עת מדעי בתחום חקר ארגונים באוניברסיטת חיפה, יו"ר ועדת ביקורת בלשכת המסחר והתעשייה, יו"ר פורום בוועדת היגוי באוניברסיטת חיפה ופעיל למען הקהילה בארגון רוטרי ובמסגרות נוספות.
בעל תואר M.B.A (בהצטיינות) במנהל עסקים, תואר B.A (בהצטיינות) מאוניברסיטת חיפה בסטטיסטיקה עם התמחות במימון, בוגר לימודי ביטוח (בהצטיינות) במגמה למפקחי רכישה בביטוח חיים במכללה לביטוח בישראל ובוגר קורס אנליסטים ומעריכי שווי מטעם המרכז להשתלמויות מאוניברסיטת בר-אילן. בנוסף, מוסמך כחתם מורשה בביטוח חיים (CLU) מטעם ה- American college והמכללה לביטוח בישראל ובעל רישיונות מטעם משרד האוצר בכל תחומי הביטוח.
מוסמך כמעריך שווי מימון תאגידי (CFV), מוסמך כאקטואר סיכוני חיים (LRA) ומוסמך כאקטואר סיכונים פנסיוניים (PRA) מטעם לשכת מעריכי השווי והאקטוארים הפיננסיים בישראל (IAVFA).
בעל ניסיון אינטנסיבי של מעל לעשור שנים בתחומי הערכות השווי וחוות דעת מומחה כלכליות ואקטואריות לבתי משפט הייעוץ הכלכלי, הכולל כתיבת חוות דעת מומחה מטעם בתי המשפט, חוות דעת מומחה מטעם הצדדים, וחוות דעת מומחה עבור משרדי עורכי דין מובילים.
לשעבר, מנכ"ל של מספר חברות בתחומי הטכנולוגיה והשירותים הרפואיים, סמנכ"ל בתאגיד בנקאי מוביל, ממונה על איסור הלבנת הון וממונה על ועדות אשראי, סמנכ"ל ומנהל מחוז בחברת ביטוח ציבורית, עיתונאי כלכלי בעל טור קבוע במגזין הכלכלי (Isr.) Forbes בתחום הניהול ושוק ההון, יו"ר דירקטוריון וחבר במספר דירקטוריונים.

משרד הייעוץ הכלכלי K.O. Dekel & Co מתמחה במתן חוות דעת מומחה כלכליות ואקטואריות לבתי משפט, להליכי בוררויות, פישור וגישור בחישוב נזקים כלכליים, אובדן רווחים, זכויות פנסיוניות, איזון משאבים בין בני זוג וכן בביצוע הערכות שווי חברות. חוות הדעת של המשרד נדונו בבתי המשפט ותקפותן ומהימנותן הוכחה. לרשות המשרד ניסיון מוכח בעדות בבתי המשפט לשם תמיכה בחוות הדעת.

רועי פולניצר הינו בעליו של חברת "שווי פנימי" המתמחה בהערכות שווי בלתי תלויות. בעשור האחרון היה רועי אחראי על אלפי עבודות הערכות שווי של חברות שונות, ייחוס עודף עלות, ייעוץ כלכלי ומידול פיננסי אשר בוצעו עבור משרדי רואי חשבון, משרדי ייעוץ כלכלי, חברות פרטיות וציבוריות בישראל.
רועי נמנע על רשימת היועצים של רשות המסים בישראל הן בתחום הערכות שווי בנושא שינוי מבנה עסקי והן בתחום הערכות שווי בנושא נכסים בלתי מוחשיים בעסקאות מקרקעין. בנוסף, רועי נמנה על רשימת המומחים הכלכליים של מספר בתי משפט בישראל (שלום ומחוזיים כאחד) בתחומי הערכות השווי והאקטואריה הפיננסית והוא משמש כמנכ"ל ויו"ר לשכת מעריכי השווי והאקטוארים הפיננסיים בישראל (IAVFA).
רועי הינו מרצה מבוקש בתחומי הערכות השווי והאקטואריה הפיננסית, המופיע בפני חברי הנהלה ודירקטורים והוא עמד בראש צוות המשימה שגיבשה את כללי האתיקה והסטנדטים המקצועיים של IAVFA כמו גם בראש פורום הפרקטיקנים שקובע את גילויי הדעת של IAVFA. בעברו שימש רועי כמרצה בקורסים מתקדמים בניתוח דוחות כספיים והערכת שווי חברות במכללה האקדמית אשקלון ובמוסדות אקדמיים שונים.
רועי בעל תואר שני במנהל עסקים (התמחות במימון) ותואר ראשון בכלכלה (התמחות במימון) מאוניברסיטת בן-גוריון ועבר בהצלחה רבה את כל ששת בחינות הרשות לניירות ערך לרישיון מנהל תיקים בישראל. כמו כן, רועי מוסמך כמעריך שווי מימון תאגידי (CFV), כמעריך שווי מימון כמותי (QFV), כמודליסט פיננסי וכלכלי (FEM), כאקטואר סיכוני שוק (MRA), כאקטואר סיכוני אשראי (CRA), כאקטואר סיכונים תפעוליים (ORA), כאקטואר סיכוני השקעות (IRA), כאקטואר סיכוני חיים (LRA), וכאקטואר סיכונים פנסיוניים (PRA), מטעם לשכת מעריכי השווי והאקטוארים הפיננסיים בישראל (IAVFA), כמנהל סיכונים מוסמך (CRM) מטעם האיגוד הישראלי למנהלי סיכונים (IARM) וכמנהל סיכונים פיננסיים (FRM) מטעם האיגוד העולמי למומחי סיכונים (GARP). רועי עבר בהצלחה רבה את שני מבחני ההסמכה הבינלאומית הכמותיים-אינטגרטיביים של GARP (EXAM PART I ו- EXAM PART II), כאשר בשניהם ציוניו דורגו באחוזון ה- 99 מבין 11,500 כלכלנים וסטטיסטקאים שנבחנו ב- 90 מדינות ברחבי העולם באותן הבחינות באותם המועדים. בנוסף, רועי בוגר קורסים מתקדמים במתמטיקה וסטטיסטיקה במסגרת לימודי תעודה באקטואריה באוניברסיטת חיפה ובוגר קורסים מתקדמים במתמטיקה ומימון לתואר שני בכלכלה באוניברסיטת בן-גוריון.
Tags: אקטואריה הערכת שווי מכירות תשואה




































































