k-Nearest Neighbors (השכן ה- k הקרוב ביותר) הינו אלגוריתם א-פרמטרי לרגרסיה ולסיווג. בשני המקרים משתנה הכניסה תלוי ב- k התצפיות הקרובות ביותר במרחב התכונות הטופולוגיות של קבוצות במרחב אוקלידי

פורסם: 11.12.19 צילום: יח"צ

מאמר מס' 6 בסדרה

• הקדמה

סדרת מאמרים זו מבוססת על נסיוני כמדען נתונים (Data Scientist) המתמחה בתחום למידת המכונה (ML- Machine Learning) בעולמות המימון הכמותי, ניהול הסיכונים הפיננסיים והאקטואריה.

חלק מהאלגוריתמים של ML למדתי בתואר הראשון שלי בכלכלה (כגון: הטיה מול שונות, בעיות רגרסיה מול בעיות סיווג, חלוקת נתונים ל- Training set ו- Testing set, נרמול נתונים, רגרסיה לינארית, Ridge, Lasso ו- Elastic Net, יישומי אלגברה לינארית בתוכנת Excel וכו'), חלק בקורסים לתואר שני בכלכלה (כגון: Dimensionality Reduction, Principle Components Analysis, K-Mean Cluster Analysis, Hierarchical Cluster Analysis ו- Time Series וכו'), חלק בתואר השני שלי במימון (כגון: Decision Trees, Random Forest, Monte Carlo Simulation, Bootstrapping, Cubic-Spline, Nelson-Siegel-Svensson וכו'), חלק למדתי בלימודי התעודה באקטואריה (המסווג הנאיבי של בייס, Overfitting, ,Underfitting Convolution and Pooling, תכנות מדעי וסטטיסטי בשפת R וכו'), חלק למדתי בלימודי התעודה בניהול סיכונים פיננסיים ועל חלק אף נבחנתי במבחנים הבינלאומיים להסמכה בתחום ניהול הסיכונים הפיננסיים FRM (כגון: רגרסיה לוגיסטית, Logit, Probit,LDA , K-Nearest Neighbor ו- Support Vector Machines וכו') ואת היתר למדתי עצמאית באינטרנט (כגון: Neural Networks, Ensemble, Bagging, Boosting, תכנות בשפת VBA וכו').

כמובן שההבנה העמוקה שלי באלגוריתמים של ML נשענת הן על הידע שלי בסטטיסטיקה (הכולל בין היתר: סוגי נתונים והצגתם באופן טבלאי וגרפי, מדדי מרכוז ומדדי פיזור, אחוזונים, מדדי קשר, התפלגות הנתונים, הסתברות פשוטה במרחב הסתברותי אחיד ובמרחב הסתברותי לא אחיד, הסתברות מותנית, נוסחת בייס, משתנים מקריים בדידים: ניסויי ברנולי, התפלגות בינומית, התפלגות פואסונית, התפלגות גיאומטרית, התפלגות היפרגיאומטרית, משתנים מקריים רציפים: התפלגות נורמלית, הסקה סטטיסטית, אמידה נקודתית, רווחי סמך, מבחני השערות וסטטיסטיקה א-פרמטרית) והן על הידע שלי בתורת הקבוצות (הכולל בין היתר: מערכות משוואות לינאריות, וקטורים ב- R^n, מטריצות ריבועיות, מטריצות אלמנטריות, מרחבים וקטורים, מרחבי מכפלה פנימית, אורתוגנליות, דטרמיננטות, ערכים עצמיים, וקטורים עצמיים, לכסון, תבניות ריבועיות, משוואות הפרשים, תכונות טופולוגיות של קבוצות במרחב אוקלידי, קבוצות קמורות, משפטי הפרדה, פונקציות קמורות וקעורות, תכונות ואפיונים, שנאת סיכון, אופטימיזציה של פונקציות עם ובלי אילוצים, משפט הפונקציות הסתומות, משפט המעטפת, משוואות דיפרנציאליות מסדרים שונים, מערכות של משוואות דיפרנציאליות ושיטות של אופטימיזציה דינאמית).

מטרתה של סדרת מאמרים זו היא להקנות לקורא הבנה מה עושים מדעני נתונים (Data Scientists) נתונים וכיצד הם יכולים לקדם את מטרות הארגון. מרבית אנשי המימון הכמותי, ניהול הסיכונים הפיננסיים והאקטואריה מכירים בכך שהם זקוקים לידע מסוים בתחום ה- ML על מנת לשרוד בעולם שבו מספר מקומות העבודה מושפע יותר ויותר מתחום זה. כיום, כל אנשי המימון הכמותי, ניהול הסיכונים הפיננסיים והאקטואריה צריכים לדעת לעשות שימוש בתוכנת Excel ולדעת לתכנת ברמה מסוימת ב- VBA. מחר כבר כל אנשי המימון הכמותי, ניהול הסיכונים הפיננסיים והאקטואריה יצטרכו לדעת לעבוד עם מאגרי נתונים גדולים (Big Data) תוך פיתוח ושימוש באלגוריתמים של ML על מנת לזהות כיוונים ומגמות בעולמי התוכן שלהם או במגוון תחומים לרוחב הארגון.

בסדרת מאמרים זו חסכתי מהקורא את השימוש בתורת הקבוצות (קרי, מטריצות ווקטורים), למרות שלעניות דעתי אלגברה לינארית חיונית ביותר על מנת להגיע להבנה עמוקה ולשליטה ברמה גבוהה ב- ML.

לסיכום, סדרת מאמרים זו מציגה את הכלים, המודלים והאלגוריתמים הפופולריים ביותר שבהם משתמשים כיום מדעני נתונים.

• סיכום המאמר הקודם: מודלים לינאריים בבעיות סיווג (רגסיה לוגיסטית ו- LDA)

רגרסיה לוגיסטית (Regression Logistic), ממש כמו רגסיה לינארית, משמשת במחקר האמפירי מזה שנים רבות. כעת הרגרסיה הלוגיסטית הופכת לכלי סיווג חשוב עבור מדעני נתונים. באופן טבעי קיימות שתי קבוצות. האחת מכונה "חיובית"; האחרת מכונה "שלילית". פונקציית הסיגמואיד (Function Sigmoid) בצורת S משמשת להגדרת ההסתברות של תצפית מסוימת 'ליפול' בקבוצה החיובית.

הליך חיפוש איטרטיבי משמש למציאת הפונקציה הלינארית של ערכי המאפיינים שכאשר מכניסים אותה לתוך פונקציית הסיגמואיד היא עושה את העבודה הטובה ביותר בהקצאת הסתברות גבוהה לתוצאות חיוביות והסתברות נמוכה לתוצאות שליליות. מקובל לסכם את תוצאות השימוש ברגרסיה לוגיסטית על נתוני סט הבדיקה (Test Set) באמצעות שימוש במטריצת הטעות (Matrix Confusion).

משעה שסיימנו לבנות את הרגרסיה הלוגיסטית, עלינו להחליט באיזה אופן ישמשו התוצאות. כך למשל, אם הרגסיה הלוגיסטית משמשת להחלטת מתן אשראי, הרי שעל מקבל ההחלטה להגדיר ערך Z מסוים. כאשר ההסתברות לקבלת תוצאה חיובית מההלוואה נאמדת כגבוהה יותר מ- Z, או אז הבקשה להלוואה מאושרת. כאשר ההסתברות לקבלת תוצאה חיובית מההלוואה נמוכה יותר מ- Z, או אז הבקשה להלוואה נדחית.

קיים יחס תחלופה בין ההצלחה לזהות הלוואות טובות לבין הצלחה לזהות הלוואות שתגענה למצב של חדלות פירעון (Default). באופן טבעי שיפור ההצלחה לזהות הלוואות שתגענה למצב של חדלות פירעון מביא להרעה בהצלחה לזהות הלוואות טובות, ולהיפך. ניתן לסכם את יחס תחלופה הזה באמצעות עקומת ה- ROC (עקומה אופיינית למסווג, Receiver Operating Characteristic Curve ) המקשרת בין שיעור החיובים האמיתיים (TPR, כלומר, רמת הביטחון או רמת הסמך ופירושו האחוז מהזמן שבו תוצאה חיובית מסווגת כחיובית) לבין שיעור החיוביים הכוזבים (FPR, רמת המובהקות ופירושו האחוז מהזמן שבו תוצאה חיובית מסווגת כשלילית).

• אלגוריתם השכן ה- k הקרוב ביותר (k-Nearest Neighbors)

אלגוריתם השכן ה- k הקרוב ביותר הינה שיטת לאמידת צפיפות. תרשים פיזור מתאר פירמה באמצעות שני משתנים מסבירים; למשל, משתנה X ומשתנה Y. הפירמה 'נופלת' איפשהו בתרשים הפיזור. בין אם נבחר מספר מסוים של חברות (הווה אומר, את k החברות הקרובות ביותר) ובין אם נגדיר רדיוס מסוים (המגדיר מעגל). הרי שהרדיוס/המעגל מייצר מספר חברות בעלות מאפייני X ו- Y דומים. לאחר מכן הפירמה מסווגת לפי הרוב; לדוגמא, אם מרבית החברות שדומות לה מבחינת מאפיינים סטטיטיים הן "הלוואות טובות", או אז גם החברה ההבדקת מסווגת ככזו.

• מדד המרחק האוקלידי (Euclidean Distance Measure)

אחת האלטרנטיבות הפשוטות לרגרסיה לינארית או לרגסיה לוגיסטית היא אלגוריתם השכן ה- k הקרוב ביותר. אלגוריתם השכן ה- k הקרוב ביותר עוסק תחילה בבחירת ערך מסוים עבור ה- k ולאחר מכן במציאת k התצפיות שהמאפיינים שלהן דומים ביותר למאפיינים שמתוכם אנו מבצעים חיזוי/סיווג.

נניח שאנו רוצים לחזות את השווי של בית פרטי בשכונה מסוימת מתוך גודל המגרש ושטח הבית במ"ר. אם נקבע ש- k שווה ל- 3, או אז יהיה עלינו לחפש בסט האימון (Training Set) שלנו את שלושת הבתים שהמאפיינים שלהם (מבחינת גודל המגרש ושטח הבית במ"ר) הם הדומים ביותר לאלו של הבית המוערך. האלגוריתם מודד את רמת הדימיון באמצעות כיול המאפיינים ולאחר מכן להשתמש במדד המרחק האוקלידי (EDM- Euclidean Distance Measure). המרחק האוקלידי בין נקודה A לנקודה B מחושב באמצעות הנוסחה הבאה:

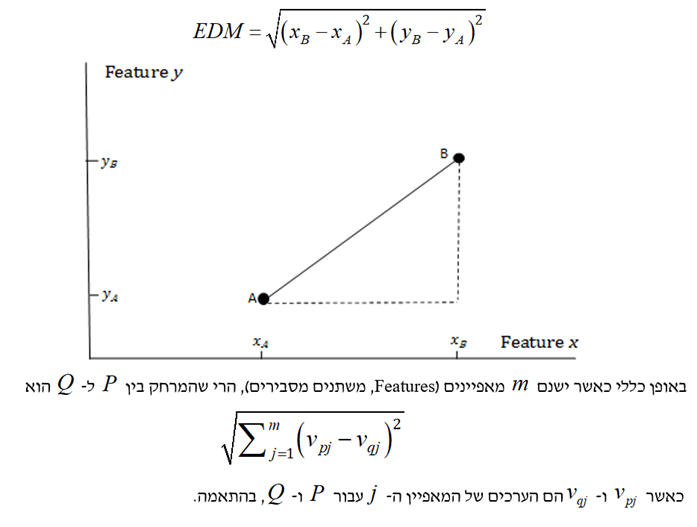
מאחר ובחרנו k שווה ל- 3, או אז עלינו לקחת את המחירים של שלושת הבתית הדומים ביותר מבחינת המאפיינים שלהם לאלו של הבית המוערך. נניח שהמחירים של שלושת הבתים הדומים ביותר (קרי, הקרובים ביותר מבחינת מדד המרחק האוקלידי) הינם 2.30 מיליון ש"ח, 2.45 מיליון ש"ח ו- 2.18 מיליון ש"ח. לפיכך, השווי של הבית המוערך הנאמד באמצעות אלגוריתם השכן ה- k הקרוב ביותר, עבור k שווה ל- 3, שווה לממוצע האריתמטי של שלושת הבתים הללו או 2.31 מיליון ש"ח.

אילו היינו בוחרים k שווה ל- 2, או אז היה עלינו לקחת את המחירים של שני הבתית הדומים ביותר מבחינת המאפיינים שלהם לאלו של הבית המוערך. נניח שהמחירים של שני הבתים הדומים ביותר (קרי, הקרובים ביותר מבחינת מדד המרחק האוקלידי) הינם 2.30 מיליון ש"ח ו- 2.45 מיליון ש"ח. לפיכך, השווי של הבית המוערך הנאמד באמצעות אלגוריתם השכן ה- k הקרוב ביותר, עבור k שווה ל- 2, שווה לממוצע האריתמטי של שני הבתים הללו או 2.375 מיליון ש"ח.

אלגוריתם השכן ה- k הקרוב ביותר יכול גם לשמש לצורך סיווג. נניח שאנו רוצים לחזות האם הלוואה מסוימת שאנחנו רוצים לתת ללווה קמעונאי מסוים תוחזר במלואה או לא מתוך ארבעת המאפיינים הבאים:

אם נקבע ש- k שווה ל- 10, או אז יהיה עלינו לחפש את 10 ההלוואות בסט האימון שלנו שהמאפיינים שלהן (מבחינת בעלות על בית, הכנסה באלפי דולר, יחס חוב להכנסה וציון אשראי) הם הדומים ביותר (קרי, הקרובים ביותר מבחינת מדד המרחק האוקלידי) לאלו של ההלוואה הנבחנת. נניח שמתוך 10 ההלוואות הדומות ביותר (קרי, הקרובות ביותר מבחינת מדד המרחק האוקלידי) שלקחנו- 8 הלוואות התבררו כהלוואות טובות (קרי, שתוצאת ההלוואה שלהן היא 1) ו- 2 התבררו כהלוואות שהגיעו לחדלות פירעון (קרי, שתוצאת ההלוואה שלהן היא 0). לפיכך, ההסתברות לחדלות פירעון (PD- Probability to Default) של ההלוואה הנבחנת הנאמדת באמצעות אלגוריתם השכן ה- k הקרוב ביותר, עבור k שווה ל- 10, שווה שווה ל- 20% (2 הלוואות שהגיעו לחדלות פירעון מתוך 10 הלוואות דומות).

אילו היינו בוחרים k שווה ל- 9, או אז עלינו לחפש את 9 ההלוואות בסט האימון שלנו שהמאפיינים שלהן (מבחינת בעלות על בית, הכנסה באלפי דולר, יחס חוב להכנסה וציון אשראי) הם הדומים ביותר (קרי, הקרובים ביותר מבחינת מדד המרחק האוקלידי) לאלו של ההלוואה הנבחנת. נניח שמתוך 9 ההלוואות הדומות ביותר (קרי, הקרובות ביותר מבחינת מדד המרחק האוקלידי) שלקחנו- 8 הלוואות התבררו כהלוואות טובות (קרי, שתוצאת ההלוואה שלהן היא 1) ורק אחת התבררה כהלוואה שהגיעה לחדלות פירעון (קרי, שתוצאת ההלוואה שלה היא 0). לפיכך, ההסתברות לחדלות פירעון (PD- Probability to Default) של ההלוואה הנבחנת הנאמדת באמצעות אלגוריתם השכן ה- k הקרוב ביותר, עבור k שווה ל- 9, שווה שווה ל- 11.11% (הלוואה אחת שהגיעה לחדלות פירעון מתוך 9 הלוואות דומות).

• לסיכום

אלגוריתם השכן ה- k הקרוב ביותר הינו אלטרנטיבה פשוטה לרגרסיה. יישום האלגוריתם כולל 3 שלבים. בשלב הראשון, מנרמלים את הנתונים (Feature Scaling). בשלב השני, מודדים את המרחק, במרחב של n מימדים, של הנתונים החדשים מהנתונים שעבורם יש לנו תוויות (Labels, תוצאות ידועות).

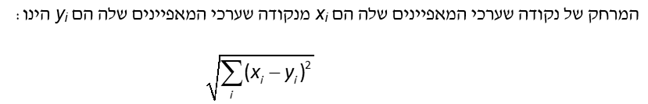
בשלב השלישי, בוחרים את k פריטי הנתונים הקרובים ביותר וממצעים את התוויות שלהם. לדוגמה, אם תחזית מכירות רכבים במדינה מסוימת בארה"ב עבור k ששווה ל- 3 ושלושת השכנים הקרובים ביותר (קרי, הקרובים ביותר מבחינת מדד המרחק האוקלידי) עבור צמיחת התוצר ושיעור הריבית נותנים לנו מכירות של 5.2, 5.4 ו 5.6 מיליון יחידות, או אז על פי אלגוריתם השכן ה- k הקרוב ביותר, עבור k ששווה ל- 3, תחזית מכירות הרכבים באותה מדינה תהיה הממוצע של התוויות של 3 השכנים הקרובים ביותר (קרי, הקרובים ביותר מבחינת מדד המרחק האוקלידי) או 5.4 מיליון יחידות. נניח שאנחנו רוצים לנבא האם הלוואה מסוימת שאנחנו רוצים להעמיד ללווה צרכני מסוים תגיע לחדלות פירעון או לא, עבור  kששווה ל- 5 וחמשת השכנים הקרובים ביותר (קרי, הקרובים ביותר מבחינת מדד המרחק האוקלידי). עוד נניח שמתוך חמש ההלוואות הדומות ביותר (מבחינת המאפיינים של ההלוואה שלנו), אנחנו יודעים שארבע הגיעו לחדלות פירעון ורק אחת הוחזרה במלואה. לפיכך, לפיכך, ההסתברות לחדלות פירעון (PD- Probability to Default) של ההלוואה הנבחנת הנאמדת באמצעות אלגוריתם השכן ה- k הקרוב ביותר, עבור k שווה ל- 5, שווה שווה ל- 80% (4 הלוואות שהגיעו לחדלות פירעון מתוך 5 הלוואות דומות).

"מדען נתונים הוא אחד שגם טוב יותר בסטטיסטיקה ואקונומטריקה מכל בוגר מדעי המחשב או מהנדס תוכנה וגם טוב יותר בהנדסת תוכנה מכל סטטיסטיקאי או כלכלן", רועי פולניצר, אקטואר ומעריך שווי, 2019.

רועי הינו מדען נתונים (Data Scientist) העושה שימוש ב- Machine Learning לצורך פיתוח מודלים מתקדמים לניהול סיכונים (בדגש על אשראי קמעונאי) כגון מודלים מנבאי התנהגות לקוחות ו/או מודלי תחזיות בתחום ניהול הסיכונים, שיפור מודלים בתחום ניהול הסיכונים, ניתוח צרכים עסקיים בעולמות ניהול הסיכונים, אפיון פתרונות מתאימים באמצעות עבודה מול בסיס נתונים גדולים ויישום כלים אנליטיים מתקדמים בעולם הבינה המלאכותית, הערכת סיכוני מודל וניטור פעולות מתקנות, ניתוח ועיבוד גורמי סיכון עיקריים, וניתוח הבדלים בין חלופות ואיפיון גורמי סיכון.

ניסיונו של רועי בתחום ה- Data Analysis, כולל: עבודה עם מאגרי מידע גדולים Big Data תוך שימוש ב- Statistical Learning (כגון: סטטיסטיקה תיאורית, הסתברות, הסקה סטטיסטית, סטטיסטיקה א-פרמטרית, חלוקת נתונים, נרמול נתונים, Fitting ו- Bayes Theorem) ובאלגוריתמים מסוג Unsupervised Learning (כגון: k-means Clustering, Hierarchical Clustering, Density-based Clustering, Distribution-based Clustering ו- Principle Components Analysis) למציאת דפוסים וזיהוי מגמות ואנומליות בעולמות ניהול הסיכונים, ההשקעות, האקטואריה, הביטוח והפנסיה, פיתוח תשתית לצורך ניתוח נתונים, שילוב והטמעת כלים לצורך גישה ושליפה עצמאית של נתונים ממאגרי מידע, פיתוח דוחות, ממשקים ומסכים באמצעות כלי ויזואליזציה.

ניסיונו של רועי בתחום ה- Data Science, כולל: עבודה עם מסדי נתונים גדולים Big Data תוך שימוש באלגוריתמים מסוג Supervised Learning (כגון: Linear Regression, Ridge Regression, Lasso Regression, Elastic Net Regression, Logistic Regression, Maximum Likelihood Estimation, k-Nearest Neighbors, Decision Tree, Random Forest, Ensemble, Bagging, Boosting, Naïve Bayes Classifier, Linear Separation, Support Vector Machine, Non-Linear Separation, SVM Regression, Artificial Neural Network, Convolutional Neural Network ו- Recurrent Neural Network) לניבוי וסיווג בעולמות ניהול הסיכונים, ההשקעות, האקטואריה, הביטוח והפנסיה ובמודלים מסוג Reinforcement Learning (כגון: Q-learning, Monte Carlo Simulation, Temporal Difference Learning ו- n-Step Bootstrapping) לקבלת החלטות מרובות שלבים בעולמות ניהול הסיכונים, ההשקעות, האקטואריה, הביטוח והפנסיה, זיהוי אתגרים עסקיים שבהםDATA  יכול להוות גורם מכריע בשיפור קבלת החלטות, איתור ואיסוף מקורות מידע, הגדרה ואיפיון של שימושי המידע, בניית מסד המידע, אפיון והגדרת הצגת המידע ותוצריו, פיתוח כלים, מודלים, תהליכים ומערכות בתחום האנליזה, תוך שימוש בכלי אנליזה מתקדמים (VBA, R Programming ו- Python).

מגזין "סטטוס" מופק ע"י: 

Tags:  הערכת שווי כספים

---