
לערבות פיננסית יש ערך כלכלי שכן היא מקטינה את עלות החוב (הריבית) עבור החברה הלווה. במאמרו משנת 1974 הראה רוברט מרטון כי שווייה הכלכלי של ערבות שקול אפקטיבית, מכל הבחינות המימוניות המהותיות, להפרש שבין הערך הנוכחי של חוב, המהוון בריבית שוק חסרת סיכון והערך הנוכחי של חוב, המהוון בריבית שוק נורמטיבית מייצגת לחברה. מר פולניצר פיתח מודל ממחושב להערכת שווי ערבויות
פורסם: 25.3.18 צילום: shutterstock
גישות להערכת ערבויות
ישנן מספר גישות המוצעות בספרות הכלכלית כפי שמופיע בציטוט מהמאמר Methods of Loan Guarantee Valuation and Accounting:
"The first method is the “rule of thumb" approach which uses the market value of the debt (or relevant underlying variables) and compares it with a risk-free asset to determine the value of guaranteeing the risky debt…The second method is the market-valuation method, where similar assets with and without guarantees are compared, and it is assumed that the market accounts for the value of the guarantee.”
ציטוט ממייל שקיבלתי מפרופ' למימון מאחת מחמשת האוניברסיטאות הגדולות בארץ.
"It is difficult to point to something in general. The value of guarantees should be derived from a structured model based on the credit spread (CDS type). It depends very much on the correlation between the guaranteed firm and the guaranteeing firm. The value of guarantees is also similar to a short position in a Put option on assets of both companies – very similar to a senior debt.”
באופן כללי יש מספר שיטות שהוצעו לאמידת ערבות אשר מפורטות במאמר הסקירה של מודי ופאטרו. הגישה הראשונה מבוססת על ניתוח אמפירי של נתוני השוק. יש עבודות האומדות את ההבדל בין שווי השוק של חוב קיים (קרי, הערך הנוכחי של תזרימי המזומנים הצפויים לנבוע מהחוב, מהוון בריבית שוק נורמטיבית מייצגת למנפיק) לבין הערך הנוכחי של החוב מהוון בריבית שוק חסרת סיכון. סוג אחר של מחקר התמקד בניתוח הפערים בין שווי נכסים כולל ערבות לבין שווי נכסים דומים ללא ערבות. בדיקות אלה הן בעייתיות בגלל מגבלת הנתונים והקושי לנטרל אפקטים אחרים על התוצאות. בדיקות אלה בוצעו בארה"ב ומרביתן על חברות מסוכנות עם סטיות תקן של שיעורי התשואה ברמות גבוהות.
גישה אחרת הינה גישת ה- CDS, לפיה ניתן לתמחר את הערבות כחוזה CDS. הרעיון הוא שהערבות מבטחת את בעל החוב מפני חדלות פירעון של הלווה, ועל כן חוזה ה- CDS על חוב מסוים אומד למעשה את ההפסד הפוטנציאלי לבעל החוב.
גישה נוספת הינה גישת האופציות, לפיה ניתן לתמחר ערבות כאופציית מכר על שווי הנכסים של הלווה. הרעיון הוא שהערבות מאפשרת לבעל החוב למכור את החוב במיוחד כאשר הוא מאבד מערכו (קרי, כאשר הלווה מגיע למצב של חדלות פירעון), ועל כן אופציית המכר על נכסי הפירמה עם מחיר מימוש השווה לערכו העתידי של החוב אומדת את ההפסד הפוטנציאלי לבעל החוב. בבסיס חישוב שווי הערבות כאופציית מכר קיימת ההנחה שהענקת אופציית מכר (במקרה זה תיאורטית) מפצה את בעל החוב על ידי הענקת זכות לבצע מכירה של החוב שברשותו במחיר השווה לערך העתידי של ההתחייבויות (קרי, סך הקרן והריבית הצבורה שהחברה הבטיחה לשלם), בעת חדלות הפירעון של הלווה (ובכך הופכת את החוב המסוכן לחוב חסר סיכון).
בעניין זה ישנן שתי גישות מקובלות לקביעת שווי הערבות – האחת, לפי גישת מרטון (1974) והשניה לפי גישת לוקאס ומקדונדלד (2006).
גישת Merton (1974)
Merton (1974) מבוסס על אומדן שווי פעילות החברה המאוחדת (על בסיס כלכלי-מאוחד), בערכים נוכחיים שנסמן אותו להלן באות V. שווי הפירמה מתחלק באופן כללי בין בעלי החוב השונים לבין מחזיקי ההון העצמי. נסמן את סך שווי החוב וההון העצמי בערכים נוכחיים כ- D ו- S, בהתאמה.
מודל מרטון בצורתו הפשוטה מניח שלחברה ישנו חוב שמשך חייו הואT שנים, ובתום T שנים החברה מתחייבת להחזיר לבעלי החוב את הקרן והריבית הצבורה שהובטחה ובסה"כ התחייבה להחזיר F. בתנאים אלה הראה מרטון שהחוב הקונצרני הינו התחייבות מותנית הניתנת להערכה כלכלית באופן הבא:

גישת Lucas and McDonald (2006)
Lucas and McDonald (2006) תוקפים את מודל Merton (1974) בגלל הנחותיו החזקות שאינן מתקיימות במציאות. ראשית, Merton מניח כי לפירמה יש רק חוב אחד לנושה אחד עם טווח לפדיון אחד, בעוד שלמרבית החברות ישנו מבנה חוב המורכב מיותר מחוב אחד, לעיתים אף מריבוי שכבות של חובות מועדפים לנושים שונים ובעלי טווחים שונים לפדיון. שנית, Merton מניח כי החוב של הפירמה מונפק בניכיון, הווה אומר, לא משלם קופונים, בעוד שחברות רבות משלמות קופונים. שלישית, Merton מניח כי קרן החוב של הפירמה נפרעת בתשלום אחד, בעוד שמרבית החברות פורעות קרן לשיעורין או באופן בלתי מסודר. כל ההנחות הללו של Merton נועדו על מנת שיוכל לתמחר ערבות כאופציית מכר אירופאית באמצעות המודל שלו Merton (1973). אולם, כיוון שחברות רבות משלמות קופונים כמו גם פורעות קרן לשיעורין, הרי שחדלות הפירעון יכולה להתרחש לפני T כאשר החברה אינה מסוגלת לעמוד בתשלום הקופון ו/או הקרן הקרוב. בנוסף בפועל, כשמצבה הפיננסי של החברה מידרדר בעלי החוב לרוב דורשים להעמיד את החוב לפירעון מיידי, או שהחברה עצמה עושה מהלך יזום ונכנסת למו"מ מול בעלי החוב.
כדי להתגבר על קושי זה Lucas and McDonald (2006) מיישמים גרסה מורחבת של מודל Merton – שבה לא רק שחדלות הפירעון יכולה להתרחש בכל שלב במהלך חיי החוב ולא רק במועד פדיון החוב כפי שמתואר במודל Merton המקורי אלא שגם ניתן לתת ביטוי לחוב המשלם קופונים ופורע קרן לשיעורין, ולא רק חוב מסוג Zero-Coupon.
על כן, Lucas and McDonald (2006) מציעים להעריך את שווייה הכלכלי של ערבות שהועמדה לטובת החברה באמצעות מודל Monte Carlo הכולל רכיב (Barrier) מסוג Knock in (Down and in) עשויה לשפר את אמידת ההפסד הצפוי לבעלי החוב, כיוון שהוא מאפשר לאירוע חדלות הפירעון להתרחש בכל עת מרגע הנפקת החוב ועד זמן T.
דוגמא מספרית להערכת שווי הוגן של ערבות מבעל שליטה נכון ל- 31 בדצמבר 2017
- כללי
חברת XXX וחברת YYYהינן חברות ציבוריות אשר מניותיהן נסחרות בבורסת תל אביב ונכון ליום ה- 31 בדצמבר 2017, מחזיקה חברת XXX ב- 13,395,690 ממניות YYY.
ביום ה- 31 בדצמבר 2017 העמיד בנק מסוים (להלן "הבנק") לחברת XXX יתרת אשראי על סך של כ- 236 מיליון ש"ח (להלן "סך האשראי"), מתוכו סך של כ- 178 מיליון ₪ בגין ערבות בנקאית שהעמיד הבנק לטובת מחזיקי איגרות החוב של חברת XXX והלוואה בסך 58 מיליון ₪ למשך תקופה של שנתיים (להלן "ההלוואה"). כעת נניח כי בעל השליטה בחברה (להלן "בעל השליטה") אשר מחזיק בכ- 80.7% ממניות החברה, העמיד לטובת החברה ערבות (להלן "ערבות") בצורת מניות YYY, בעבור סך של 60 מיליון ₪ (12.5 ₪ למניה), במידה וחברת XXX לא תפרע לבנק את חובה בגין ההלוואה עד לתום התקופה כאמור על-ידי מכירת 4.8 מיליון מניות YYY המוחזקות על-ידי חברת XXX, או היה והבנק יעמיד לפירעון מיידי את סך האשראי שהעמיד לחברת XXX.
ההסכם בין חברת XXX ובין הבנק קובע כי מניות המוחזקות ע"י חברת XXX ישועבדו לטובת סך האשראי (להלן "המניות המשועבדות"). המניות המשועבדות כוללות בעיקר את החזקת חברת XXX במניות חברת YYY (למעט 4.8 מיליון המניות אשר עליהן מוטל שיעבוד קבוע) ו- 2,715,119 ממניות ZZZ שגם היא חברה ציבורית אשר מניותיה נסחרות בבורסת תל אביב, וכן בניירות ערך סחירים אחרים. ההלוואה מובטחת ע"י שעבוד שוטף של כל נכסי חברת XXX וכן ע"י שעבוד קבוע על 4.8 מיליון מניות YYY המוחזקות ע"י חברת XXX. מניות YYY ו- ZZZ מהוות את עיקר המניות המשועבדות ושימשו, לפיכך, כמייצגות את תיק המניות המשועבדות כולו.
לפי הנהלת חברת XXX, ההסכם קובע כי סך האשראי יועמד לפירעון מיידי, במידה ויפחת שווי המניות המשועבדות, במועד כלשהו לאורך השנתיים המהוות את תקופת ההלוואה, מיתרת סך האשראי (לאחר הניכויים כדלהלן), כאשר יתרת סך האשראי לאחר הניכויים מוכפלת ב- 80% (להלן "סכום הסף"). הניכויים מיתרת סך האשראי הם: ערבות אישית שניתנה על ידי בעל השליטה לטובת סך האשראי (37% אחוז מיתרת סך האשראי), והתמורה שאמורה להתקבל ממימוש הערבות (60 מיליון ₪).
בדוגמא מספרית זו נבצע הערכת שווי כלכלי לערבות, שנתן בעל השליטה לחברת XXX, למכירת 4.8 מיליון מניות YYY, תמורת 60 מיליון ₪, ליום 31 בדצמבר 2017 (להלן "מועד ההערכה").
- מתודולוגיה
לצורך הערכת שווייה ההוגן של הערבות אשר הועמדה לטובת החברה על ידי בעל השליטה, נדרש לעשות שימוש במודל גמיש ועל כן בחרנו להשתמש במודל Monte Carlo גמיש, הנחשב לאחד מטכניקות ההערכה המקובלות לתמחור ערבויות.
סימולציית Monte Carlo – שיטה לפתרון בעיות חישוביות באמצעות מספרים אקראיים. בחרנו להשתמש במודל זה מכיוון שהוא המתאים ביותר להערכת שווי ערבות, המהווה מכשיר פיננסי מורכב, בו גלומים גורמי סיכון שונים התלויים במספר נכסים שונים.
סוג הסימולציה הנפוץ ביותר עבור נכסים פיננסיים מורכבים הינו סימולציית Monte Carlo. סימולציית Monte Carlo בנויה על דגימה מקרית של גורמי סיכון מהתפלגות מתאימה. על סמך הדגימה נוצרים מסלולים דמיוניים של שינויים בגורמי סיכון לאורך זמן.
שיטת Monte Carlo היא שיטה לפתרון בעיות חישוביות באמצעות מספרים מקריים. למרות המקריות שבמספרים המקריים, השיטה מאפשרת להגיע לרמת דיוק נדרשת על ידי שימוש בחוק המספרים הגדולים.
בהתאם לכך, בונים תזרים מזומנים וסדרת החלטות לכל מסלול ומסלול. ממוצע של תזרימים אלו על כל המסלולים מהוון בשיעור הריבית חסרת הסיכון, מהווה קירוב לשווי הערבות.
רמת הדיוק של השיטה נמדדת על ידי פרמטר שנקרא Standard error of sample mean אשר מהווה אינדיקציה לאיכות התוצאה.
במקרים שבהם מעורבות תכונות אמריקאיות (אפשרות למימוש אופטימאלי לפני הפקיעה) יש גרסאות מורכבות יותר של סימולציות Monte Carlo.
מודל Merton אינו מתאים להערכת שווי הערבות, מאחר ובמקרה דנן שלפנינו ישנו יותר ממועד מימוש אפשרי אחד. הוא הדין לגבי המודל התרינומי, הואיל והערבות תלויה במחירו של יותר מנכס אחד (מניית YYY, המניות המשועבדות והמניות המהוות את נכסיו העיקריים של בעל השליטה).
יישום סימולציית Monte Carlo במקרה דנן שלפנינו מביא בחשבון את:
- מועד הכניסה של הערבות לתוקף כתלות בהעמדת האשראי לפרעון מיידי עקב ירידת שווי המניות המשועבדות מסכום הסף.
- שווי נכס הבסיס של הערבות (מניות YYY) במועד הכניסה לתוקף.
- שווי המניות המרכיבות את נכסי בעל השליטה המשמשים כבטוחה למימוש הערבות.
על מנת לאמוד את השווי הכלכלי של הערבות תוך שימוש בסימולציית מונטה-קרלו, נדרש להשתמש במספר משתנים עבור כל מניה אשר בגינה מורצת הסימולציה:


על מנת לאמוד את שווייה הכלכלי של הערבות, נבצע 5,000 הרצות של סימולציית מונטה-קרלו על מחירי המניות הרלבנטיות להערכה. בכל הרצה, מחירי המניות הרלבנטיות להערכה נאמדו לשמונה מועדים (להלן "מועדי המדידה"), החל ממועד ההערכה ועד לתום שנתיים ממועד זה (סיום תקופת ההלוואה), במרווחים רבעוניים.
תוצאת כל הרצה תהא מטריצה של מחירי המניות הרלבנטיות להערכה על פני מועדי המדידה ולכל הרצה נחשב את שווי הערבות תחת מטריצת מחירי המניות.
אמידת שווייה הכלכלי של הערבות, תוך שימוש בסימולציית מונטה-קרלו, תכלול בתוכה התייחסות לפרמטרים הבאים:
שווי נכס הבסיס במועד ההערכה ("Spot") – במידה והחברה ציבורית, שווי נכס הבסיס יהיה מחיר השוק של המניה ליום ההערכה.
- תוספת המימוש של הערבות ("Strike") – תוספת המימוש של הערבות היא הסכום שישולם על ידי בעל השליטה בעת מימוש הערבות על ידי הבנק.
- תקופת הערבות – תקופת הערבות היא התקופה שבין מועד ההערכה ובין מועד המימוש הצפוי.
- שיעור הריבית חסרת הסיכון – שיעור הריבית חסרת הסיכון הוא התשואה המשתמעת הזמינה באופן שוטף של אגרות חוב ממשלתיות, הנושאות ריבית נקובה בשיעור אפס, של המדינה שבמטבע שלה מבוטא מחיר המימוש, כאשר יתרת התקופה שלהן שווה לתקופה הצפויה של האופציה המוערכת. ככל ששיעור הריבית חסרת הסיכון גבוה יותר, כך שווי הערבות קטן.
- שיעור תשואת הדיבידנד הצפוי – מכיוון שמחיר המניה משקף את עליית ערכה הפוטנציאלי של המניה וכן את תשלומי הדיבידנדים העתידיים, הרי שעל שווייה הכלכלי של הערבות לשקף את היעדר דיבידנדים אלו ("תשואת דיבידנד"). ככל ששיעור תשואת הדיבידנד הצפוי גבוה יותר, כך שווייה הכלכלי של הערבות גדל. במקרה של חברה שאינה מחלקת ואינה צופה חלוקת דיבידנדים, או לחילופין במקרה בו נקבע בהסכם הערבות כי תוספת המימוש של הערבות מותאמת לתשלומי דיבידנד, ייקבע שיעור תשואת דיבידנד של אפס.
- סטיית התקן של נכס הבסיס – סטיית התקן החזויה של תשואת המניה מחושבת בהתבסס על מדידת התנודתיות ההיסטורית של תשואת המניה הרלבנטית להערכה, בהתאם ליתרת אורך החיים החוזי של הערבות. סטיית התקן הצפויה של תשואות המניה הינה מדד לשיעור הממוצע שבו צפויות לחול תנודות בתשואות המניה במהלך התקופה. סטיית התקן המשמשת במודלים לתמחור אופציות הינו סטיית התקן השנתית של שיעורי התשואה של המניה בחישוב רציף על פני תקופת זמן. סטיית התקן מבוטאת, באופן רגיל, במונחים שנתיים, מבלי להתחשב בתקופת הזמן ששימשה בחישוב, לדוגמה, תצפיות יומיות, שבועיות, או חודשיות. ככל שגדלה סטיית התקן הצפויה כך גדל הפוטנציאל לעליית נכסי הפירמה, ולכן לערבות המוענקת על נכסי הפירמה ישנו ערך גבוה יותר, תיאורטית, מאשר לערבות המוענקת על נכסי הפירמה שפחות תנודתיים. באמידת סטיית התקן הצפויה יש לשקול את סטיית התקן הגלומה מתוך מחירי שוק של מכשירים סחירים קיימים של החברה, סטיית התקן היסטורית של מחיר המניה על פני תקופה התואמת את התקופה הצפויה של הערבות, משך הזמן שבו מניית החברה נסחרת בציבור ועוד.
- המתאם בין המניות הרלבנטיות להערכה – המתאם בין תשואות המניות הרלבנטיות להערכה משמש לאמידת מחירי המניות במסגרת בניית מטריצות המחירים. המתאם בין תשואות המניות הרלבנטיות להערכה מחושב בהתבסס על נתונים היסטוריים של מחירי מניות אלו, בהתאם ליתרת אורך החיים החוזי של הערבות.
- כניסת האופציה לתוקף – במסגרת יישום סימולציית מונטה-קרלו להערכת שווי ערבות, תיבדק עבור כל הרצה של הסימולציה, כניסת הערבות לתוקף לכל אחד ממועדי המדידה על בסיס מטריצת מחירי המניות המשועבדות שתתקבל מהרצת הסימולציה. בהתאם לכך, יבדק לכל מועד מדידה האם שווי המניות המשועבדות גבוה יותר מסכום הסף, אם לאו.
במידה שבמועד מדידה מסוים, שווי המניות המשועבדות היה נמוך יותר מסכום הסף, תיבדק הכדאיות של מימוש הערבות באמצעות השוואת תוספת המימוש (12.5 ₪ למניה) למחיר מניית YYY החזוי לאותו מועד.
במידה ומחיר מנית YYY החזוי נמוך יותר מ- 12.5 ₪, הרי שקיימת כדאיות כלכלית במימוש הערבות, שווי הערבות יחושב כהפרש שבין התמורה שתתקבל ממימוש הערבות (60 מיליון ₪) לבין שווי 4.8 מיליון מניותYYY בהתאם למחירן החזוי לאותו מועד.
כמו כן, נלקח בחשבון סיכון חדלות הפירעון של בעל השליטה. בהתאם לכך, הוערכה יכולתו של בעל השליטה לפרוע את התשלום בגין תוספת המימוש של הערבות באמצעות המחירים החזויים של מניות YYY, ZZZ ו- WWW (חברת WWW, גם היא חברה ציבורית אשר מניותיה נסחרות בבורסת תל אביב), המהוות, לפי מידע ציבורי, את נכסיו העיקריים של בעל השליטה (מניית WWW מוחזקת בשיעור של כ- 70.2% על-ידי בעל השליטה. YYY ו- ZZZ מוחזקות באמצעות חברת XXX. חברת XXX ביחד עם חברת CCC מהוות, לפי מידע ציבורי, את נכסיו העיקריים של בעל השליטה). כיוון שחברת XXX מחזיקה במניות YYY ו- ZZZ הרי שאם נחזה את מחיריהן בשל היותן המניות המשועבדות, נוכל להשתמש במחירי המניות הללו על מנת להעריך את שווי החזקותיו של בעל השליטה בחברת XXX.
התזרים הצפוי (payoff) מהערבות יהוון למועד ההערכה לפי שיעור הריבית חסרת הסיכון, כאשר שווי הערבות יחושב על-ידי מיצוע התוצאות שיתקבלו בכל הרצות הסימולציה שיערכו.
- הנחות עבודה
- שווי נכס הבסיס במועד ההערכה ("Spot") – במידה והחברה ציבורית, שווי נכס הבסיס יהיה מחיר נכס הבסיס של הערבות הינו 4.8 מיליון מניות YYY. על פי שער הסגירה ביום 31.12.2017 בבורסה לניירות ערך בתל אביב, מחיר מניית YYY עמד על 8.24 ₪. מכאן, ששווי נכס הבסיס עמד על 39.6 מיליון ₪.
- מחירי וכמויות המניות הנוספות – כמות מניות YYY המוחזקות על ידי חברת XXX (למעט 4.8 מיליון המניות המהוות את מכפיל נכס הבסיס) הינה 8,595,690. על פי שער הסגירה ביום 31.12.2017 בבורסה לניירות ערך בתל אביב, מחיר מנית ZZZ עמד על 7.68 ₪. כמות מניות ZZZ המוחזקות על ידי חברת XXX הינה 2,715,119. על פי שער הסגירה ביום 31.12.2017 בבורסה לניירות ערך בתל אביב, מחיר מנית WWW עמד על 11.09 ₪. מספר המניות הנפרעות של WWW הינו 31,914,833.
נכון למועד ההערכה, בעל השליטה מחזיק בכ- 80.7% ממניות YYY ו- ZZZ המוחזקות על ידי חברת XXX ובכ- 70.2% ממספר המניות הנפרעות של WWW.
- תוספת המימוש של הערבות ("Strike") – תוספת המימוש של הערבות הינה 60 מיליון ₪ תמורת 4.8 מיליון מניות YYY, כלומר, מחיר של 12.5 ₪ למניית YYY.
- תקופת הערבות – משך חיי הערבות הוא הנמוך מבין התקופה עד להעמדת האשראי לפירעון מיידי לבין תקופה של שנתיים ממועד ההערכה, לפי תקופת ההלוואה.
- שיעור הריבית חסרת הסיכון – הואיל ותוספת המימוש של הערבות איננה צמודה למדד המחירים לצרכן – עשינו שימוש בריבית נומינלית חסרת סיכון בישראל. הטבלה הבאה מציגה את וקטור הריביות הנומינלי חסר הסיכון בישראל, כפי שפורסם על ידי "שווי פנימי", נכון ל- 31.12.2017:
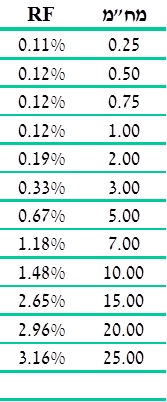
לצורך חישובינו השתמשנו בשיעור ריבית חסרת סיכון הנגזר מוקטור הריביות הנומינלי חסר הסיכון בישראל, המחושב על בסיס איגרות חוב לא צמודות של ממשלת ישראל. שיעור הריבית הריאלית חסרת הסיכון שבו השתמשנו הינו 0.19%.
- שיעור תשואת הדיבידנד הצפוי – כיוון שנקבע בהסכם, כי תוספת המימוש של הערבות תותאם לתשלומי דיבידנד, קבענו כי שיעור תשואת הדיבידנד הצפוי על המניות הינו 0%.
- סטיית התקן של נכס הבסיס – הטבלה הבאה מציגה את סטיות התקן החזויות של מניות YYY, ZZZ ו- WWW, אשר שימשו לביצוע סימולציית Monte Carlo:
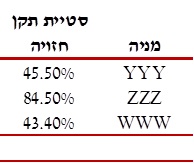
- המתאם בין המניות הרלבנטיות להערכה – הטבלה הבאה מציגה את המתאמים בין תשואות מניות YYY, ZZZ ו- WWW, אשר שימשו לביצוע סימולציית Monte Carlo:
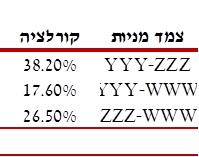
- תוצאות הערכת השווי
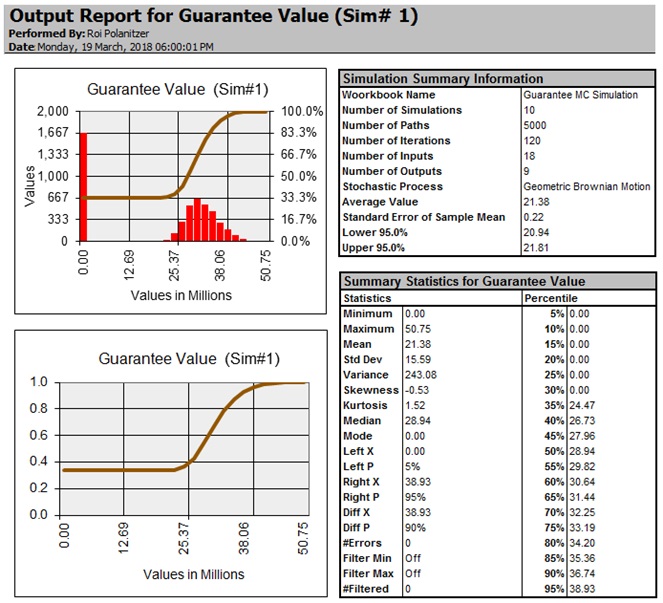
להערכתנו ועל בסיס חישובינו, שווייה הכלכלי של הערבות שהעמידה בעל השליטה לחברת XXX, נאמד ליום 31.12.2017 בטווח של כ- 20.94-21.91 מיליון שקלים חדשים (בתוחלת כ- 21.38 מיליון שקלים חדשים).
הטבלה הבאה מציגה את שווייה הכלכלי של הערבות נכון למועד ההערכה:
דוגמא מספרית להערכת שווי כלכלי של ערבות בעלים למצבת האשראי של החברה ל- 28 במרץ 2018
- כללי
חברת "אשד – המפל הקטנטן" (להלן "החברה") עוסקת בפעילות יזמית, בעיקר בתחום הבנייה למגורים ובביצוע עבודות בנייה בכל רחבי הארץ. החברה בפנקס הקבלנים ובעלת רישיון מסוג ג-5, המאפשר לה לבצע עבודות בנייה בהיקף בלתי מוגבל.
רכישת מקרקעין על ידי החברה מתבצעת בדרך של השתתפות במכרזים של מנהל מקרקעי ישראל ורכישות מגופיפ פרטיים. לצורך מימון הפרויקטים אותם היא מקימה, מתקשרת החברה עם בנקים בהסכמי ליווי בנייה (להלן "הסכמי הליווי"). הסכמי הליווי מבוססים על שיטת "פרויקט סגור", בהם מתקשרת החברה עם הבנק נותן האשראי בהסכם, המבטיח לחברה את מכלול השירותים הפיננסיים הנצרכים על ידה במהלך חיי הפרויקט, לרבות הוצאת ערבויות לרוכשי הדירות בהתאם לחוק המכר (דירות) (הבטחת השקעות של רוכשי דירות), התשל"ה-1974. החברה מממנת את פעילותה בעיקר באמצעות אשראי בנקאי וכן על ידי הון עצמי. כנגד האשראי הבנקאי משעבדת החברה הן את נכסיה והן את הנכסים הנמכרים על ידה. בעלי השליטה בחברה ערבים אישית להתחייבות החברה בגין ניצול האשראי בפועל המשמש לפעילותה.
ביום ה- 27 בפברואר 2018 (להלן "מועד ההקמה") חברת אשד פרסמה תשקיף, לפיו הוצעו לציבור 80,000,000 איגרות חוב בנות 1 שקל חדש ערך נקוב רשומות על שם, במחיר של 90% מערכן הנקוב לפירעון בארבעה תשלומים שנתיים שווים, ביום 1 לחודש מרץ של כל אחת מהשנים 2021 עד 2024 (כולל) (להלן "אגרות החוב"). איגרות החוב נושאות ריבית שנתית בשיעור של 7% (במופע חצי שנתי) צמודות (קרן וריבית) למדד המחירים לצרכן בגין חודש ינואר 2018. הריבית על איגרות החוב משולמת ביום 1 לחודשים ספטמבר ומרץ של כל אחת מהשנים 2018 עד 2024 (כולל).
ביום ה- 1 במרץ 2018 נטלה החברה הלוואה בסך 100,000 ₪ המגובה בערבות בעליה. תקופת ההלוואה הינה 4 שנים, והריבית הנקובה בהלוואה הינה 7.5% לשנה. לוח הסילוקין של ההלוואה הינו פשוט למדי ומורכב מארבעה תשלומים: 7,500 ₪ בשנה הראשונה, 7,500 ₪ בשנה השנייה, 7,500 ₪ בשנה השלישית, ו- 107,500 ₪ בשנה הרביעית. ההלוואה איננה צמודה למדד המחירים לצרכן.
- מתודולוגיה
הערבויות אשר ניתנו לחברה על ידי בעלי מניותיה (להלן "ערבויות הבעלים") מהוות, מכל הבחינות הכלכליות המהותיות, הטבה כלכלית בידי החברה. בהתאמה, שווייה של ההטבה השוטפת בתקופת הדיווח נאמד כפער שבין עלות המקורות (אשר אינם מגובים בערבות על ידי בעלע מניות החברה ואינם מובטחים בבטוחות בהיקף ובשיעור דומה לאשראי הבנקאי), בה גייסה החברה או הייתה עשויה לגייס חוב פיננסי, לבין העלות האפקטיבית של מקורות החוב הפיננסי שניצלה החברה בפועל.
הפרש עלויות גיוס מימון זה מהווה את שווייה הכלכלי של ערבות הבעלים. לפיכך, שווייה הכלכלי של ערבות הבעלים למצבת האשראי שלה ליום 31 בדצמבר 2017, נאמדה כההפרש בין הערך הנוכחי של ההלוואה הבנקאית, המהוון במחיר החוב הנורמטיבי לחברה, נטול ערבויות ושעבודים והערך הנוכחי של ההלוואה הבנקאית, המהוון בריבית בגין חוב מובטח בליווי ובגיבוי ערבויות בעלים.
- הנחות עבודה
- מחיר החוב הנורמטיבי לחברה – בהיעדר תצפיות בדבר שיעורי תשואה נומינליים נורמטיביים לחברה, שיעור ההיוון אשר שימש בעבודתנו לחישוב ערכה הנוכחי של ההלוואה, נאמד על בסיס שיעור התשואה לפדיון הגלום באיגרות החוב הצמודות למדד המחירים לצרכן של החברה ליום המסחר הראשון שלהן בבורסה לניירות ערך בתל אביב (7 במרץ 2018). שיעור זה נאמד על ידינו בכ- 8.59%.
לשם קירוב המרתו של האחרון לשיעור תשואה נומינלי נורמטיבי מייצג לחברה, אמדנו בנוסף את ההפרש בין התשואה לפדיון של איגרת חוב ממשלתית שקלית (סדרה 1122) לבין התשואה לפדיון של איגרת חוב ממשלתית צמודה (סדרה 0922) הצמודה למדד המחירים לצרכן. סך הצברם של שיעורי התשואה כאמור לעיל עמד על 9.92% ושימש אותנו בחישובינו כאומדן למחיר חוב נורמטיבי (נומינלי) לחברה, נטול ערבויות ושיעבודים.
- ריבית בגין חוב מובטח בליווי ובגיבוי ערבויות בעלים – כאמור הריבית השנתית הנקובה בהלוואה עומדת על 7.5% והיא מהווה אומדן לריבית בגין חוב מובטח בליווי ובגיבוי ערבויות בעלים.
- תוצאות הערכת השווי
הסכום שגויס באמצעות הערבות עמד על 100,000 ₪, הסכום שניתן היה לגייס ללא ערבות הינו 92,316 ₪ ועל כן שווייה הכלכלי של הערבות הוא 7,684 ₪.
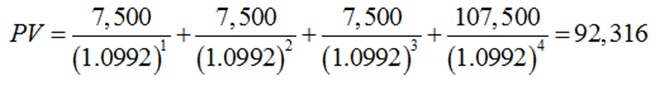
הערכת שווייה הכלכלי של הערבות בשיטה שהוצגה לעיל דורשת את אמידתו של מחיר חוב נורמטיבי לחברה הנערבת. במידה ולחברת הנערבת אין איגרות חוב סחירות ואין דירוג פומבי, או אז מלאכת מחיר חוב נורמטיבי לחברה הנערבת יכולה להיות מאוד מורכבת.
- לסיכום
ערבות הינה מוצר מורכב, המאופיין בתכונות רבות המקשות על הערכת שוויו. וכן בנוסף, הפרמטרים הדרושים לתמחור אינם חד משמעיים (לדוגמה הקורלציה בין רמת הסיכון של נכסי הנערב לבין רמת הסיכון של נכסי הערב). מר פולניצר פיתח מודל ממחושב להערכת שווי ערבויות פיננסיות וערבויות בעלים – המהוות את אחד המכשירים המורכבים להערכת שווי.
אנו מבצעים הערכת שווי של נכסים מורכבים שונים לפי מספר מודלים המקובלים בתחום. בין היתר, אנו משתמשים במודל של Lucas ו- McDonald (2006) לתמחור ערבויות. מודל זה ניתן ליישום על ידי שימוש ב- סימולציית מונטה קרלו או על ידי עצים תרינומיים. מדובר במודל המקובל כיום בעולם לתמחור ערבויות.
אנו בשווי פנימי מעדיפים להשתמש בטכניקת סימולציית Monte Carlo, המבוססת על סימולציה מקרית של גורמי סיכון מרכזיים לצורך גזירת שווי כלכלי של נכסים פיננסים באמצעות התפלגות סיכון נייטרלית (Risk Neutrality).
שיטת Monte Carlo הנה שיטה אלגוריתמית לפתרון בעיות חישוביות באמצעות הרצת פרמטרים סטוכסטיים, במספר רב של מצבי עולם וביצוע חישובים על התרחישים השונים אשר התקבלו. שימוש בשיטה זו נהוג במקרים בהם אין אפשרות דטרמיניסטית למדל את מושא המחקר.
הערכת שווי ערבויות באמצעות מודל זה ניתן ליישום על ידי שימוש ב- סימולציית מונטה קרלו או על ידי עצים תרינומיים.
לצורך הערכת שווי ערבויות, אנו בשווי פנימי משתמשים באחד משני התהליכים הסטוכסטיים המקובלים.
הראשון הינו תהליך סטוכסטי מסוג Geometric Brownian Motion (GBM) כדלקמן:

השני הינו תהליך סטוכסטי מסוג Jump Diffusion כדלקמן:

השימוש במספר תהליכים סטוכסטיים בסימולציית Monte Carlo מאפשר לנו ניתוח השוואתי של התוצאות טרם הגשת חוות דעת ללקוח, וזאת על מנת להקטין את סיכון המודל. חוות הדעת שלנו כוללת, בין היתר:
- רקע תיאורטי
- תיאור המודלים להערכת שווי
- תיאור הפרמטרים שבהם נעשה שימוש
- ניתוחי רגישות לתוצאות בהתאם לרמות שונות של פרמטרים, אשר לגביהם לא קיימת וודאות מלאה (לדוגמה: הקורלציה בין רמת הסיכון של נכסי הנערב לבין רמת הסיכון של נכסי הערב, סטיית התקן של נכסי הערב, ועוד).
תוצר העבודה הסופי שלנו הינו ברור, תמציתי ומציג את מסקנות העבודה בצורה הטובה ביותר, מה שמאיץ את תהליך הביקורת וממזער את הסחת דעתה של ההנהלה.

מעריך השווי מטעם קלמנוביץ עסקים ומשפט: יועץ ההשקעות אילן קלמנוביץ, QFV
מעריך השווי הראשי של קלמנוביץ עסקים ומשפט, יועץ ההשקעות אילן קלמנוביץ', בעל הסמכות מעריך שווי מימון תאגידי (CFV), מעריך שווי מימון כמותי (QFV) ומודליסט פיננסי וכלכלי (FEM) מטעם לשכת מעריכי השווי והאקטוארים הפיננסיים בישראל (IAVFA), בעל רישיון עורך דין בישראל מטעם לשכת עורכי הדין בישראל, בעל רישיון יועץ השקעות מטעםהרשות לניירות ערך ובעל רישיון מגשר מטעם הנהלת בתי המשפט.

משרד קלמנוביץ עסקים ומשפט חבר בלשכת מעריכי השווי והאקטוארים הפיננסיים בישראל (IAVFA) ומתמחה במתן שירותים כלכליים ו- משפטיים, לחברות, לעסקים ולפרטיים, בתחום האזרחי, המסחרי והכלכלי, למגוון רחב של צרכים הן בעסקים והן במשפט, כשהוא עושה שימוש בידע וניסיון רב תחומי שנצברו אצלו במהלך השנים (One Stop Shop). בתחום העסקים המשרד מציע שירותי הערכות שווי לחברות, לעסקים ולניירות ערך, חוות דעת כלכליות להליכים משפטיים, ליווי עסקי וכלכלי בעסקאות M&A, בוררויות וגישורים בסכסוכים עסקיים. בתחוםהמשפט המשרד מציע שירותי שירותי ייצוג בתחום האזרחי, המסחרי והכלכלי, תביעות ייצוגיות, נגזרות והגבלים עסקיים, יעוץ וליווי משפטי בעסקאות M&A, בוררויות וגישורים בסכסוכים עסקיים וסיוע בחקירות של מומחים כלכליים וחשבונאיים. שירותי הייעוץ הכלכליים ניתנים ללקוחות באמצעות חברת ייעוץ בבעלות מייסד המשרד – לידרס ייעוץ וניהול בע"מ, כפוף לכללי האתיקה של לשכת עורכי הדין בישראל.

מעריך השווי האחראי מטעם שווי פנימי: האקטואר רועי פולניצר, QFV
מנכ"ל לשכת מעריכי השווי והאקטוארים הפיננסיים בישראל (IAVFA) ובעליו של משרד הייעוץ הכלכלי שווי פנימי – מעריכי שווי בלתי תלויים, האקטואר רועי פולניצר, בעל הסמכות מעריך שווי מימון תאגידי (CFV), מעריך שווי מימון כמותי (QFV), מודליסט פיננסי וכלכלי (FEM), אקטואר סיכוני שוק (MRA), אקטואר סיכוני אשראי (CRA), אקטואר סיכונים תפעוליים (ORA), אקטואר סיכוני השקעות (IRA), אקטואר סיכוני חיים (LRA) ואקטואר סיכונים פנסיוניים (PRA) מטעם לשכת מעריכי השווי והאקטוארים הפיננסיים בישראל (IAVFA), בעל הסמכת מנהל סיכונים פיננסיים (FRM) מטעם האיגוד העולמי למומחי סיכונים (GARP) ובעל הסמכת מומחה לניהול סיכונים (CRM) מטעם האיגוד הישראלי למנהלי סיכונים (IARM).

שווי פנימי – מעריכי שווי בלתי תלויים
משרד הייעוץ הכלכלי שווי פנימי – מעריכי שווי בלתי תלויים חבר בלשכת מעריכי השווי והאקטוארים הפיננסיים בישראל (IAVFA) ומתמחה הן בציטוט של מטריצות ריביות להיוון מכשירים (נכסים והתחייבויות) פיננסיים והתחייבויות פנסיוניות והן במתן ייעוץ כלכלי וניתוחים כמותיים במכשירים פיננסיים ובמדידת סיכונים לצורכי יישום הוראות רגולטוריות, תקינה חשבונאית, פיתוח, יישום ותיקוף מודלים בתחומי האקטואריה, ניהול הסיכונים, והערכות שווי למטרות מס, עסקאות, דוחות כספיים ולצרכים משפטיים. בין לקוחות המשרד נמנים, בין היתר, משרדי רואי חשבון, משרדי ייעוץ כלכלי וחברות פרטיות וציבוריות בארץ.
Tags: אקטואריה הערכת שווי כלכלה פיננסים תשואה




































































