מידול פיננסי וכלכלי – מאמר מס' 7 בסדרה: ה- VaR (שווי הוגן בסיכון, Value at Risk) אומד את ההפסד המקסימלי הצפוי להשקעה בודדת או לתיק השקעות בשל התממשות סיכוני השוק בהינתן אופק זמן ורמת ביטחון סטטיסטית שנקבעו מראש. משמעותו של VaR יומי של מיליון ₪ ברמת ביטחון של 99%, היא שבמהלך 24 השעות הקרובות הסיכון שנפסיד יותר ממיליון ₪ קטן  מ- 1%

פורסם: 22.2.18   צילום: shutterstock

 

הגדרת השווי ההוגן בסיכון VaR

ה- VaR (שווי הוגן בסיכון, Value at Riskׂ) נועד להשיב על השאלה מהו ההפסד המקסימלי הצפוי מהשקעה מסוימת או שמתיק השקעות מסוים, על פני אופק זמן מוגדר, אשר לא יעלה מעל לרמת ביטחון נתונה. למשל, "תחת תנאי שוק נורמליים, ההפסד המקסימלי שתיק ההשקעות יכול להפסיד על פני חודש אחד הינו כ- 3.6 מיליון ₪ ברמת ביטחון של 99%", הווה אומר, "תחת תנאי שוק נורמליים, ההפסד המקסימלי שתיק ההשקעות יכול להפסיד על פני חודש אחד הינו כ- X ₪ או X% ברמת ביטחון של(1 – α) ".

למעשה ניתן לפרש את ה- VaR בשני אופנים. פעם אחת, ה- VaR הוא ההפסד המקסימלי שנצפה להפסיד ברמת ביטחון נתונה על פני אופק זמן מסוים. ופעם שניה, ה- VaR הוא הפסד המינימלי שנצפה להפסיד ברמת מובהקות נתונה (קרי, המשלים ל- 1 של רמת הביטחון) על פני אופק זמן מסוים.

 

חישוב ה- VaR

ברגיל, ה-VaR  מחושב בהנחת התפלגות נורמלית כמכפלה של גודל התיק (Pׂ) בסטיית התקן היומית (סיגמא) ובמספר סטיות התקן (z). כך למשל, עבור רמת ביטחון של 95% (חד זנבי) הערך המתאים ל- z הינו 1.65.

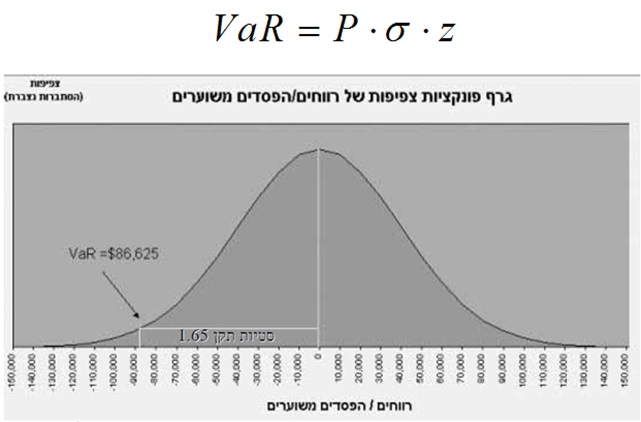
השאלה הראשונה שעולה היא מהו אופק הזמן הראוי לצורך חישוב VaR? התשובה לשאלה זו נגזרת מהתשובה לשתי השאלות הבאות: הראשונה, כמה זמן אני מתכונן להחזיק את הפוזיציה? פעילות למסחר (בנקים) או חשיפה פסיבית (חברות). השניה, באיזה מהירות ניתן להנזיל את הפוזיציה? נזילות השוק או תהליך קבלת ההחלטות. נציין רק כי עבור תקופות ארוכות, כלומר, מעל יום אחד יש להשתמש במכפלה של שורש הזמן (אומדן בלבד עבור נכסים לינאריים כאשר מדובר בהתפלגות נורמלית).

השאלה השנייה שעולה היא מהי רמת הביטחון הסטטיסטית הראויה לצורך חישוב VaR? על פי רוב, רמת הביטחון המקובלת נעה בין 95% ל- 99%. כך למשל, עבור התפלגות חד זנבית רמת ביטחון של 95% שקולה ל- 1.65 סטיות תקן (קרי, יום אחד מתוך 20 ימי מסחר), רמת ביטחון של 97.5% שקולה ל- 1.96 סטיות תקן (קרי, יום אחד מתוך 40 ימי מסחר) ורמת ביטחון של 99% שקולה  ל-2.33 סטיות תקן (קרי, יום אחד מתוך 100 ימי מסחר), כאשר אסור לשכוח שכאשר מדובר בהתפלגות השונה מהתפלגות נורמלית הרי שקיים סיכון עודף ב'זנבות'.

השאלה השלישית שעולה היא עד כמה יש 'ללכת אחורה' בעת קביעת סטיית התקן לצורך חישוב ה-VaR? כעיקרון ההנחה הבסיסית היא שהעבר מייצג, אבל איזה עבר? השנה האחרונה או חמש השנים האחרונות? ובנוסף האם משקלה של כל אחת מהתצפיות בחלון הזמן שנבחר צריך להיות זהה? מחד גיסא, עדיף לקחת כמה שיותר תצפיות, הואיל ואז המדגם יותר מייצג. זוהי גם העדפת רשויות הפיקוח הואיל והיא נתמכת אקדמית. מאידך, אין לקחת יותר מדי תצפיות הואיל ופעם אחת השווקים משתנים ופעם שניה סטיות התקן והקורלציות אף הן משתנות על פני זמן. לעניין משקל התצפיות, אחד הפתרונות לכך הוצע על ידי בנק ההשקעות J.P MORGAN והוא מדבר על שקלול אקספוננציאלי לצורך חישוב סטיית התקן העתידית (מודל ה- EWMA).

 

מגבלות כלליות של VaR

למרות שמודלים של VaR משמשים כ'קו הגנה ראשון' כנגד סיכונים פיננסיים, עלינו להכיר גם את מגבלותיהם. המגבלה הראשונה הינה סיכון יציבות, הווה אומר, העבר אינו בהכרח מלמד על העתיד. המגבלה השניה הינה סיכון תקופת מעבר, משמע, סיכון הנובע משינויים ארגוניים, כניסה למוצרים או שווקים חדשים, יישום מערכות מיכון חדשניות ויישום הוראות פיקוח חדשות. המגבלה השלישית הינה שינוי בפוזיציות, למשל במהלך תקופת החזקה של 10 ימים יכולים לחול שינוים בפוזיציה כגון: הגדלת פוזיציה או גידול בהפסד הצפוי. המגבלה הרביעית הינה פוזיציות שאין להם מחירי שוק. והמגבלה החמישית היא סיכון מודל, למשל שימוש במודל 'בלק אנד שולס' כאשר ההנחות לא מתקיימות במציאות וכשהפרמטרים לא נאמדו נכון (הלא אך טבעי שככל שישנם יותר פרמטרים כך אנו מאבדים יותר דרגות חופש והסיכון הולך גדל).

 

בדיקת נאותות (Backtesting) של מודל ה- VaR

כדי לבדוק את נאותות המודל יש לבדוק את שיעור הכישלון, כלומר, להשיב על את בכמה מקרים ההפסד בפועל חרג מה- VaR היומי.

Backtesting או בעברית "בדיקה חוזרת" הינו תהליך הבוחן את מהימנות מודל ה- VaR אשר במסגרתו חושב מספר הפעמים בו ההפסד בפועל (כהגדרת המונח להלן) היה גדול מערך ה- VaR שחושב, ונערכה השוואה למספר ההפסדים שאמורים היו להיווצר לתיק לפי רמת המובהקות עבורה חושב ערך ה- VaR.

"הפסד בפועל" – בודק את הרווח וההפסד של התיק בהינתן הפוזיציה למועד המדידה, על פי מחירי גורמי הסיכון כפי שהתממשו ביום המסחר הראשון שלאחר מדידת ה- VaR.

חריגה מוגדרת כהפרש בין הפסד בפועל (כהגדרת המונח לעיל) לבין ערך ה- VaR. במצב שההפסד בבדיקה החוזרת נמוך יותר מערך ה- VaR, לא קיימת חריגה.

המלומד Paul Kupiec פיתח רווח בר סמך בהתאם להתפלגות חי בריבוע עם דרגת חופש אחת תחת השערת האפס ש- p היא ההתפלגות הנכונה ו- N הוא מספר התצפיות.

 

 

מבחני מאמץ (Stress Testing) למודל ה- VaR

מבחני מאמץ בודקים את מודל ה- VaR תחת תנאי שוק קיצוניים חלף תחת תנאי שוק נורמליים, כלומר, להתמודד עם מצבים שלא משתקפים בהיסטוריה עליה נבנה מודל ה- VaR.

ברגיל, תרחיש הקיצון מחושב לתקופה ארוכה יותר (בדרך כלל תקופה של 3 שנים אחרונות) ובנוסף כולל גם נתונים מתקופת משבר (למשל את כל נתוני שנת 2008 – שנת משבר האשראי). ישנם פרקטיקנים שנוהגים לקחת בנוסף רמת בטחון של 100% (כך למשל, עבור רמת ביטחון של 100% הערך המתאים ל- z הינו 7.94).

המלומד Philippe Jorion מציע להשתמש במבחני המאמץ שאר אומצו על ידי ה- Derivatives Policy Group כגון: שינוי מקביל בעקום התשואה לפדיון 1%±, שינוי בצורת עקום התשואות 0.25%±, שינוי בשע"ח 6%± ושינוי בשונות 20%±.

כמובן שראוי לאמץ מבחני מאמץ בהתאם לנתונים הכלכלים. לסיכום ניתן לומר כי מבחני מאמץ יעילים בלבחון את המצב הגרוע ביותר של גורמי הסיכון העיקרים.

 

דוגמה לחישוב VaR עבור משקיע אירופאי

משקיע אירופאי רוכש אג"ח על סך 140 מיליון דולר ל-10 שנים. כלומר, הוא LONG דולר SHORT יורו – הוא נהנה מפיחות של היורו ביחס לדולר, משמע הוא חשוף לתיסוף של היורו ביחס לדולר. אם נניח כי שער החליפין הינו 1.4 דולר ליורו, רמת הביטחון הינה 95%, מספר סטיות התקן המתאים לרמת ביטחון של 95% הוא 1.65, מקדם המתאם בין סיכון שע"ח לסיכון הריבית הוא 0.27-, סטיית התקן היומית של שע"ח היורו-דולר היא 0.565% סטיית התקן היומית של הריבית (מחיר האג"ח) היא 0.605%.

 

 

דוגמה מספרית נוספת

נניח שיש לנו תיק השקעות בסך של 2 מיליון ₪. 50% ממנו מושקעים בתעודות סל על מדד ת"א 35 עם ס.ת. יומית של 1% ו- 50% הנותרים מושקעים במק"מ עם סטיית תקן של 0.1%. נניח כי הקורלציה (מקדם המתאם) בין מדד ת"א 35 למק"מ הינו 0.2+.

 

מערכת לניהול הסיכונים

 

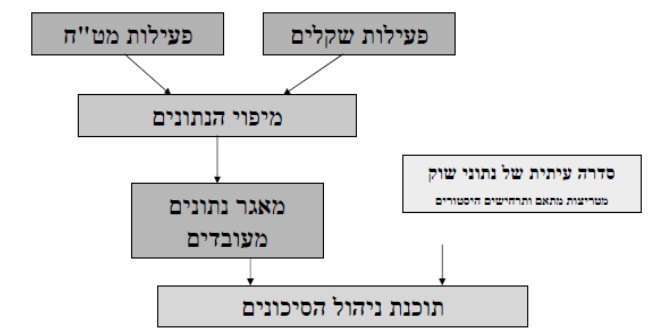
גישות שונות לחישוב VaR

ברגיל, קיימות שלוש גישות לחישוב VaR.

הגישה הראשונה נקראת גישת ההתפלגות הנורמלית (Variance-Covariance). גישת ההתפלגות הנורמלית מניחה כי תשואות הנכסים מפולגות נורמלית ועל כן היא עוסקת בחישוב קורלציות וסטיות תקן לצורך בחינת כיוון הקשר בין הפוזיציות בתיק. בגישה זו אנו מחשבים את סטיית התקן של התיק או סטיית התקן המצרפית, כאשר בחינת השינוי הבלתי צפוי נעשית ברמת ביטחון מסוימת. יתרונותיה של גישה זו הינם פשטותה, קיומה של מטריצת 'שונות-שונות משותפת' כמו גם מידת הקלות שבה ניתן לבצע ניתוחי רגישות בגישה זו. חסרונותיה של הגישה הינם הנחת הנורמליות אשר לא תמיד מתקיימת, קיומם של אירועים קיצוניים ואי יכולתה להתמודד עם נכסים א-לינאריים (כמו אופציות ואג"ח). לסיכום, גישה ההתפלגות הנורמלית מתאימה לתיק גדול המפוזר היטב.

 

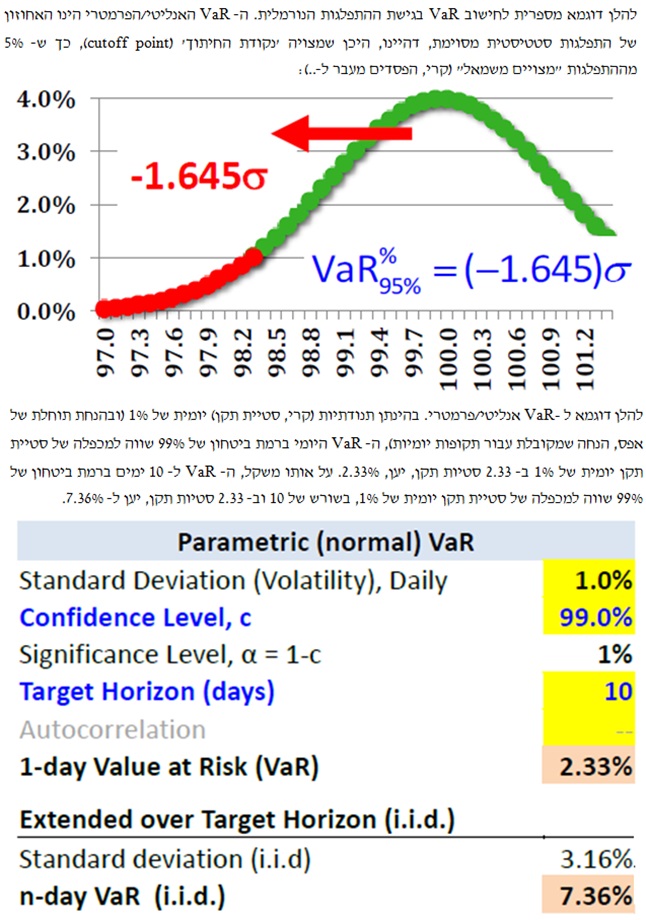
הגישה השניה נקראת גישת התרחישים ההיסטוריים (Historical Simulation). בגישת התרחישים ההיסטוריים אנחנו לא מניחים התפלגות כלשהי, אלא פשוט מתייחסים להתפלגות העבר. למעשה אנו בודקים את שוויו של התיק בהסתמך על הפוזיציה כיום ומחירים שונים בעבר, על ידי בחינת הערכים הקיצוניים של שווי התיק עבור מחירי עבר שונים ביחס לשוויו כיום. יתרונותיה של גישה זו נעוצים בהיעדר הנחת התפלגות ובאפשרותה להתמודד עם נכסים א-לינאריים. חסרונותיה של הגישה הינם דרישתה לקיומו של מאגר נתונים גדול, המשקל הרב שהיא מעניקה לתוצאות מופרזות כמו גם הקושי הנלווה לביצוע ניתוחי רגישות בגישה זו. לסיכום, גישת התרחישים ההיסטוריים מתאימה להתפלגות שאיננה נורמלית ולתיק הכולל אופציות.

להלן דוגמא מספרית לחישוב VaR בגישת התרחישים ההיסטוריים.

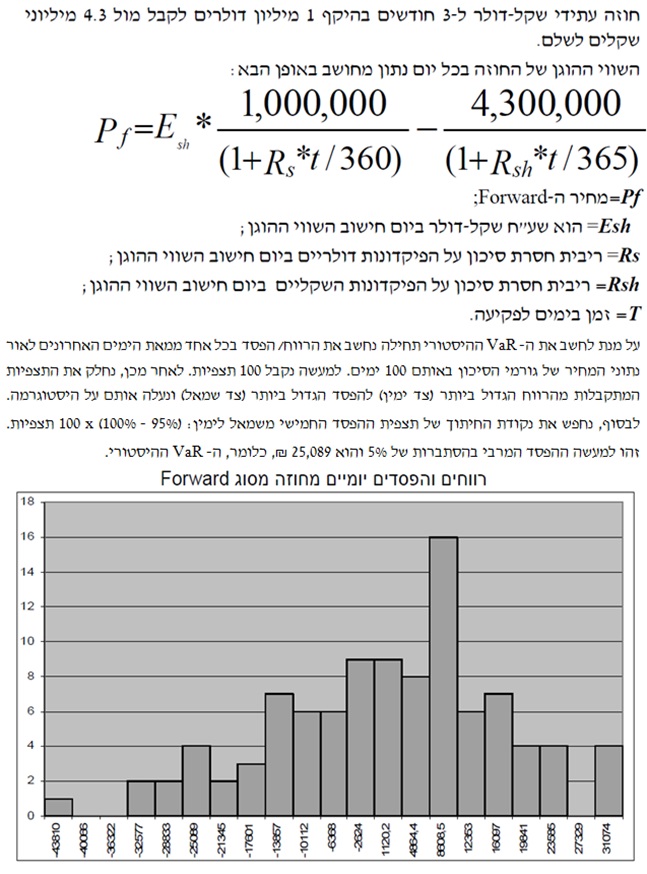
הגישה השלישית נקראת גישת התרחישים של מונטה קרלו (Monte Carlo Simulation). בגישת התרחישים של מונטה קרלו אנו מניחים התפלגות מסוימת ומגרילים תרחישים רבים באמצעות לוח מספרים מקריים הבנוי על אותה התפלגות. מהתרחישים המתקבלים אנו גוזרים רווחים והפסדים על התיק הקיים ובוחנים את הערכים הקיצוניים של שווי התיק ביחס לשוויו היום, ממש כמו בגישת התרחישים ההיסטוריים. יתרונותיה של גישה זו הינם מידת התאמתה לטיפול בסיכונים נוספים ולהתמודדות עם מכשירים מורכבים כמו גם מידת הקלות שבה ניתן לבצע ניתוחי רגישות בגישה זו. חסרונותיה של הגישה הינם דרישתה למשאבי מחשב גדולים, סיכון המודל הטבוע בה וכמובן המורכבות הנלווית להסברת הגישה ותוצאותיה. לסיכום, גישת התרחישים של מונטה קרלו מתאימה לתיק מורכב, כאשר הגורמים והפרמטרים המשפיעים על תשואות הנכסים בתיק הינם ידועים.

 

 

 

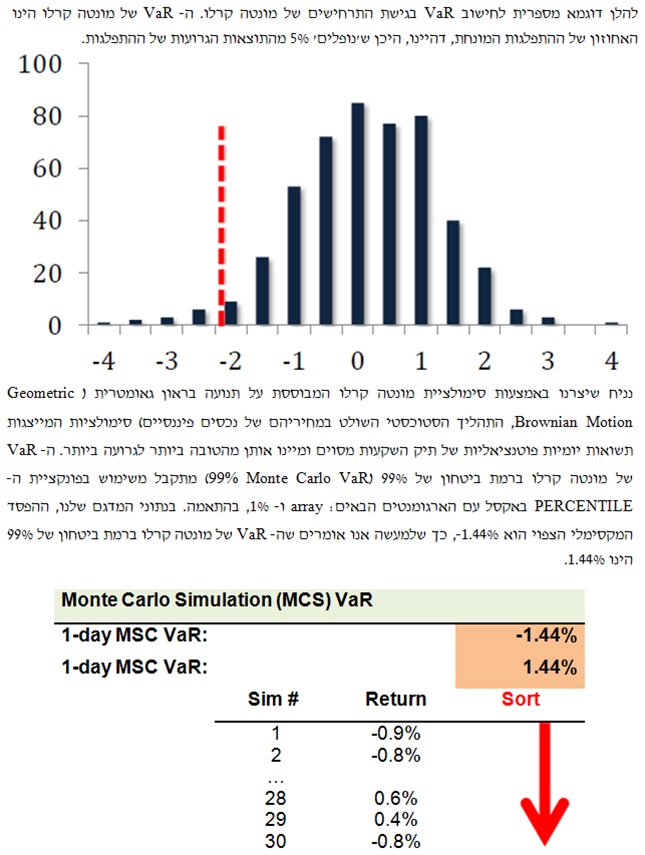
השוואה בין כלים שונים של אקטואריית סיכונים

למעט אתגר אחד בלבד (קרי, לא קל לחשב VaR), אנו מוצאים את השווי ההוגן בסיכון (VaR) ככלי העדיף ביותר על כל הכלים האחרים.

• הוראות לעצירת הפסד (stop-loss limits): אם ההפסד המצטבר שנגרם על ידי הסוחר עולה או חורג ממגבלה מסוימת, או אז יש לסגור את הפוזיציה. הבעיה הבולטת היא שההוראות הללו מיושמות ex-post (בדיעבד ולאחר מעשה).
• מגבלה על היקף (notional limit): מגבלה ex-ante (צופה פני עתיד או לפני מעשה) על היקף החשיפה. למרות שמדובר בהוראה ex-ante, הקרן איננה אמד טוב לחשיפה.
• חשיפות (exposures): מגבלות המוטלות על רגישויות; למשל, מגבלת על משך הזמן או מגבלה על הביתא. לעניות דעתי. גישה זו איננה שלמה הואיל והיא אינה מתחשבת לא בסטיות התקן של גורמי סיכון, אשר עשויות להשתנות על פני השווקים, ולא בקורלציות בין אותם גורמי סיכון, שגם הן משתנות על פני זמן.

 

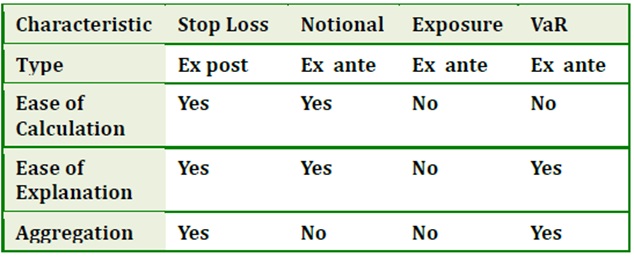
הערכות שווי לעומת אקטואריית סיכונים

במובן מסוים, ה- VaR מרחיב את השיטות להערכת שווי מכשירים נגזרים. אולם, בעוד שהערכת השווי עוסקת בחישוב התוחלת המדויקת של ההתפלגות, הרי שאקטואריית סיכונים עוסקת בחישוב השינוי המשוער של ההתפלגות, דהיינו, ערך כלשהו בזנב ההתפלגות.

המשך במאמר הבא….

 

 

*למען גילוי נאות רועי פולניצר הינו מומחה בינלאומי לניהול סיכונים אשר שימש במשך למעלה מ- 4 שנים כעוזר מחקר של המלומד ה"ה ד"ר שילה ליפשיץ, רו"ח ז"ל בתחום ניהול הסיכונים בבנקאות הישראלית.  ליפשיץ ופולניצר חקרו  מודלים של VaR ולמעשה המחקר האמפירי הראשון בישראל שבדק את ערכי ה- VaR המדווחים על ידי הבנקים בישראל ופורסם כמאמר אקדמי הינו מאמרם של ליפשיץ ופולניצר (2008). המאמר מבוסס, רובו ככולו, על עבודת הסמינריון שהגיש מר פולניצר לד"ר ליפשיץ במסגרת לימודי התואר השני שלו במנהל עסקים באוניברסיטת בן-גוריון בנגב. המאמר האמור עבר שיפוט ע"י ד"ר דן וייס ונמצא ראוי לפרסום בגיליון מיוחד מטעם מכון יוסף קסירר למחקר בחשבונאות באוניברסיטת תל אביב, אשר נשלח לכל מנכ"לי הבנקים בישראל לרבות לנגיד בנק ישראל, דאז, פרופ' סטנלי פישר. מלבד מודלים של Market VaR (פרמטרי/אנליטי, היסטורי ומונטה-קרלו), ליפשיץ ופולניצר חקרו בין היתר גם מודלים של Credit VaR (הן כנגד סיכון חדלות פירעון במתודת KMV והן כנגד סיכון הגירת אשראי במתודת CreditMetrics), מודלים של Operational VaR (בגישת LDA), מודלים של Liquidity-adjusted VaR (בגישת המרווח הקבוע, בגישה האקסוגנית ובגישה האנדוגנית), את מודל ה- LaR (קרי, Liquidity-at-Risk המכונה גם CFaR), מודלים של Investment VaR (בודד מול תיק, מבוזר מול לא מבוזר, VaR שולי, VaR רכיבי ו- VaR תוספתי) וכן את מודל ה- SaR (קרי, Surplus-at-Risk).

 

אריאל ברקי, יועץ השקעות ואקטואר סיכוני שוק FRM

מר ברקי הינו בעל ידע וניסיון רב בתחום ניהול הסיכונים הפיננסיים וייעוץ ההשקעות, מר ברקי פעיל בתחומי שוק ההון ובתחומי הייעוץ ובעבר עסק בפעילות ברוקראז' בחדרי מסחר בבנקים הגדולים בארץ, כיועץ השקעות בבנק יהב לעובדי המדינה בע"מ, כמנהל קשרי לקוחות בחברת תמיר פישמן השקעות בע"מ וכיועץ השקעות בבנק מרכנתיל דיסקונט בע"מ.

מר ברקי הינו יועץ השקעות מוסמך בישראל בעל תואר M.B.A במנהל עסקים עם התמחות במימון ושוק ההון מהמכללה האקדמית אונו, תואר B.A (בהצטיינות) בניהול מהאוניברסיטה הפתוחה, דיפלומה בניהול סיכונים פיננסיים מאוניברסיטת אריאל בשומרון, הסמכת מנהל סיכונים פיננסיים (FRM) מטעם האיגוד העולמי למומחי סיכונים (GARP) והסמכות מעריך שווי מימון כמותי (QFV), אקטואר סיכוני שוק (MRA), אקטואר סיכוני אשראי (CRA), אקטואר סיכונים תפעוליים (ORA) ואקטואר סיכוני השקעות (IRA) מטעם לשכת מעריכי השווי והאקטוארים הפיננסיים בישראל (IAVFA).

Tags:  אסטרטגיה אקטואריה הערכת שווי תשואה

---