קבוצת הסיכונים העיקרית להם חשופים הבנקים הינה סיכוני אשראי. הסתברות לחדלות פירעון מייצגת את הסבירות שלווה לא יוכל לעמוד בהחזר מלא של תשלומי קרן או ריבית בהלוואה שנטל ובכך יגיע בראיית הבנק למצב של חדלות פירעון
פורסם: 4.6.15 צילום: shutterstock
בשנת 2010 החיל בנק ישראל על הבנקים בישראל את תקן באזל II, שהינו הסטנדרט הבינלאומי הראוי לניהול סיכונים בבנקים. כפועל יוצא מכך הבנקים נדרשים להקצות הון כ"כרית ביטחון" לספיגת הפסדים בלתי צפויים, בהתאמה לסיכונים אשר להם הם חשופים.
ניתוח הלימות ההון כנגד החשיפה לסיכונים הינו כלי חשוב ומשמעותי, לא רק בשל העובדה שהוא נגזר מחובת הציות להוראות בנק ישראל, אלא גם מכך שהוא מאפשר לבנקים לבצע אופטימיזציה של ההון באמצעות חישוב הון כלכלי ( Economic Capital-EC), להקצות סיכונים, למדוד ביצועים ותשואה מותאמת לסיכון על ההון (RAROC – Risk Adjusted Return On Capital)), להוציא לפועל החלטות אסטרטגיות, להגדיל את התחרותיות ולשפר את הרווחיות.
קבוצת הסיכונים העיקרית להם חשופים הבנקים הינה סיכוני אשראי. לצורך חישוב הקצאת הון כנגד סיכוני אשראי הבנקים עושים שימוש במודלים לדירוג פנימי (IRB- Internal Ratings Based). מודלים אלו מביאים בחשבון מספר פרמטרים לצורך קביעת ההפסד הצפוי: ההסתברות לחדלות פירעון (PD – Probability of Default), חשיפה בעת חדלות פירעון (EAD – Exposure At Default) והפסד בהינתן חדלות פירעון (LGD – Loss Given Default).
סדרת מאמרים זו עוסקת בגישות מדעיות שונות לאקטואריה פיננסית הדרושות לצורך יישום גישת ה- IRB, כמו גם מודלים ומתודולוגיות ליישום והערכת ההון הכלכלי ( Economic Capital-EC), הערך הנתון בסיכון (VaR- Value at Risk), ההסתברות לחדלות פירעון (PD- Probability of Default), וההפסד בהינתן חדלות פירעון (LGD- Loss Given Default), הרכיבים העיקריים הנדרשים בגישת ה- IRB, באמצעות השימוש בניתוחים מתקדמים כגון סימולציית מונטה קרלו וסימולציה היסטורית, אופטימיזציה של תיק, חיזוי סטוכסטי וניתוח אופציות.
במקום להתעכב על תאוריה או לחזור מחדש על מה שכבר נכתב פעמים רבות, סדרת מאמרים זו מתמקדת אך ורק ביישומי המידול הפרקטי של הרכיבים העיקריים של תקן באזל II/III. המאמר הראשון בסדרה יעסוק במודלים מבניים (Structure Models) לאמידת ההסתברות לחדלות פירעון.
ההסתברות לחדלות פירעון
הסתברות לחדלות פירעון מייצגת את הסבירות שלווה לא יוכל לעמוד בהחזר מלא של תשלומי קרן או ריבית בהלוואה שנטל ובכך יגיע בראיית הבנק למצב של חדלות פירעון. הסתברות זו זהה בין אם מדובר בהלוואה מהבנק ובין אם מדובר באיגרת חוב לציבור ואינה מביאה בחשבון את הרכב וטיב הבטחונות הניתנות למימוש. ככל שהבנק אומד את ההסתברות לחדלות פירעון כגבוהה יותר, כך ידרוש שיעור ריבית גבוה יותר עבור ההלוואה כפיצוי עבור הסיכון וכמובן בטחונות נוספים.
מודלים לאמידת ההסתברות לחדלות פירעון מסווגים כמבניים (structural) או כאמפיריים (empirical). מודלים מבניים בוחנים את יכולת החברה הלווה לשרת את החוב בהתבסס על נתוני שוק כגון: מחירי המניות של החברה, שווי השוק של נכסיה, עלותו הפנקסנית של החוב בספריה, מרווחי האשראי הגלומים באיגרות החוב שהנפיקה, כמו גם סטיות התקן של משתנים אלו. לפיכך, מודלים מבניים משמשים בעיקר לאמידת ההסתברות לחדלות פירעון של תאגידים (מסחריים ותעשייתיים) ומדינות, כאשר יתרונם נעוץ בעובדה שהם מבוססים על נתוני שוק המתעדכנים על בסיס יומי.
מודלים אמפיריים או מודלים לניקוד אשראי (credit scoring) משמשים על מנת לקבוע כמותית את ההסתברות שהלוואה או לווה יגיעו לחדלות פירעון (הכוונה בלווה היא לפרט בודד) בהתבסס על נתונים סטטיסטיים המבוססים על תצפיות עבר להלוואות היסטוריות, ואמידת מאפיינים אישיים, (כגון: גיל, רמת השכלה, יחס חוב להכנסה, ומשתנים אחרים), מה שהופך את הגישה השנייה לרלוונטית יותר עבור מגזר הבנקאות הקמעונאית.
מודלים מבניים לאמידת ההסתברות לחדלות פירעון
המודלים המבניים הינם קטגוריה של מודלים האומדים את הסבירות לחדלות פירעון של החייב. המודלים המבניים נבדלים מהמודלים לניקוד אשראי במספר אופנים. ראשית, המודלים לניקוד אשראי רלוונטיים יותר עבור לווים קטנים – פרטים או עסקים קטנים בעוד שהמודלים המבניים רלוונטיים יותר עבור לווים גדולים – תאגידים ומדינות. המודלים לניקוד אשראי בחלקם הגדול הינם מודלים סטטיסטיים, המריצים רגרסיות לוגיסטיות מול מדדי סיכון שונים (כגון: הכנסת החייב, סטטוס שוכר דירה או בעל דירה, מספר השנים באותה משרה, רמת השכלה, ויחס חוב להכנסה), כמשתנים מסבירים, ביחס לאירועים של חדלות פירעון. בניגוד למודלים לניקוד אשראי, המודלים המבניים ממדלים (חוזים או מנבאים מסלולי התנהגות עתידיים) באופן ישיר את תהליך חדלות הפירעון, בהתבסס על נתוני שוק כגון: מחירי המניות של החברה, שווי השוק של נכסיה, עלותו הפנקסנית של החוב בספריה, מרווחי האשראי הגלומים באיגרות החוב שהנפיקה, כמו גם סטיות התקן של משתנים אלו.
למודלים המבניים קיימים יישומים רבים במוסדות פיננסיים. כך למשל, הם משמשים לתמיכה בניתוח אשראי ולמציאת ההסתברות לכך שפירמה כלשהי תגיע למצב של חדלות פירעון, לחילופין להערכת סיכוני האשראי של צד נגדי לעסקת נגזרות פיננסיות מעבר לדלפק (OTC- Over the Counter) או לחילופי חילופין ליישום טכניקות של הנדסה פיננסית לפיתוח נגזרי אשראי (CDS – Credit Default Swap) או מכשירי אשראי אחרים.
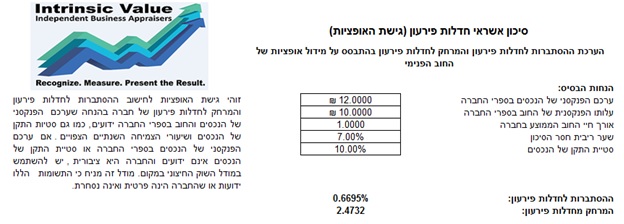
תצלום המסך הבא מציג את השימוש במודל מרטון (1974) לאמידת ההסתברות לחדלות פירעון. מודל זה משמש לצורך קבלת פתרון אנליטי לבעיית ההסתברות לחדלות פירעון של חברה ציבורית נסחרת, בעלת מבנה חוב המורכב ממניות וחוב, בהתחשב בסטיות התקן שלה בשוק (תרשים 1). מודל זה משמש כיום הן את חברת KMV והן את חברת Moody's בביצוע ניתוח סיכוני אשראי. גישה זו מבוססת על ההנחה כי ערכם הפנקסני של הנכסים בספרי החברה וסטיית התקן הנכסית אינם ידועים ומתקבלים כפתרון מהמודל, וכן שהחברה הינה יחסית יציבה וכי שיעורי הצמיחה של נכסיה הינם יציבים על פני זמן (קרי, החברה איננה חברת-הזנק).
תרשים 1 מודל ההסתברות לחדלות פירעון עבור חברות ציבוריות
המודל המוצג עושה שימוש בו זמנית במספר משוואות הנגזרות מתורת תמחור האופציות בשילוב עם אופטימיזציה לקבלת שווי השוק של נכסי החברה (Implied Value) וסטיית התקן הנכסית (Implied Volatility) וכל זאת במטרה לחשב המרחק של החברה מחדלות פירעון (Distance to Default) ובהתאם לכך את ההסתברות שלה להגיע לחדלות פירעון.
דוגמא ראשונה: מודלים מבניים לאמידת ההסתברות לחדלות פירעון עבור פירמות ציבוריות
על מנת להריץ את המודל (תרשים 1), הזנו את שווי השוק של ההון העצמי של החברה (המתקבל ממכפלת מחיר המניה בשוק במספר המניות הנפרעות של החברה), סטיית התקן ההונית של החברה (המחושבת על בסיס שיעור תשואה שבועי במשך 52 שבועות עד למועד ההערכה), עלותם הפנקסנית של ההתחייבויות והחוב בספרי החברה (המחושבים כסך הצברם של החוב לטווח ארוך למערכת הבנקאית ולגופים פיננסיים אחרים ושל חלק החוב השוטף בגין אגרות החוב והחזר ההלוואות לבנקים), אורך חיי החוב הממוצע בחברה (המחושב או כמח"מ הממוצע המשוקלל לפי שווי השוק של חובות החברה, או פשוט להזין 1 עבור תקופת ההסתברות השנתית לחדלות פירעון) ושער הריבית חסר הסיכון (המחושב כשיעור הריבית חסרת הסיכון בשוק המקומי המתאים לאורך חיי החוב הממוצע בחברה). הפרמטרים המשמשים במודל לתמחור אופציות מוצגים בתאים G18 עד G23. כל התשומות הללו מחושבות פרט לשווי הנכסים (קרי, שווי השוק של הנכסים) וסטיית התקן הנכסית. עלינו להזין אומדנים גסים כערכים טנטטיביים (ראשוניים ולא מחייבים), כך שניתן יהיה להריץ את הניתוח. כלל האצבע הוא לקבוע את סטיית התקן הנכסית בתא G22 כחמישית עד כמחצית מסטיית התקן ההונית המחושבת בתא G10, ואת שווי הנכסים (G19) כסך הצברם של שווי השוק של ההון העצמי ועלותם הפנקסנית של ההתחייבויות והחוב בספרי החברה (G9 וG11-).
לאחר מכן, יש להריץ אופטימיזציה באמצעות פונקציית ה- SOLVER באקסל על מנת לקבל את התפוקות הרצויות. על מנת לעשות זאת, נקבע כי שווי הנכסים וסטיית התקן הנכסית הינם משתני ההחלטה (Decision Variables) במודל ועל כן נקליד בפונקציית ה- SOLVER באקסל גבול תחתון של 1 ₪ עבור שווי הנכסים ו- 1% עבור סטיית התקן הנכסית כך ששתי התשומות הללו יוכלו לקבל רק ערכים חיוביים. לאחר מכן, נקבע את תא G28 כתא פונקציית המטרה, שאותה אנו רוצים להביא למינימום תחת שני אילוצים. האילוץ הראשון הוא ששווי אופציית הרכש (Callׂ) חייב להיות שווה לשווי השוק של ההון העצמי. האילוץ השני הוא שמכפלת שווי השוק של ההון העצמי בסטיית התקן ההונית חייבת להיות שווה למכפלת יחס הגידור של אופציית הרכש (Callׂ) בשווי הנכסים ובסטיית התקן הנכסית. כעת, כל מה שנותר הוא להריץ אופטימיזציה באמצעות פונקציית ה- SOLVER באקסל.
אם למודל יש פתרון, הרי שפונקציית המטרה שבתא G28 תתכנס לאפס (תרשים 1). מכאן, ההסתברות לחדלות פירעון (הנמדדת באחוזים) והמרחק לחדלות פירעון (הנמדד בסטיות תקן) מחושבים בתאים G34 ו-G36 . לאחר מכן, ניתן לחשב את תוחלת שיעור ההשבה הצפוי (G38), שווי השוק של החוב (G40) ומרווח האשראי הרלוונטי (G42). התוצאות מצביעות על כך שלחברה שבדוגמא ישנה הסתברות לחדלות פירעון של 0.87% וכי החברה מצויה במרחק של 2.38 סטיות תקן מחדלות פירעון, מה שמעיד על איכות אשראי טובה (תרשים 2).
תרשים 2 תוצאות המודל לאחר האופטימיזציה
דוגמא שנייה: מודלים מבניים לאמידת ההסתברות לחדלות פירעון עבור פירמות פרטיות
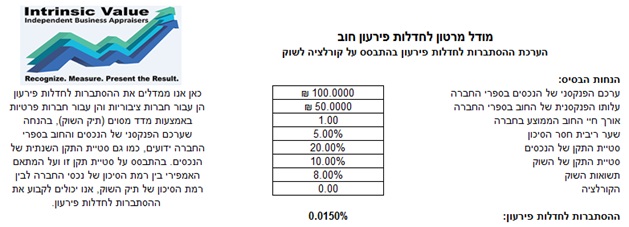
בנוסף, ישנם מודלים מבניים אחרים לחישוב ההסתברות לחדלות הפירעון של פירמה. מודלים ספציפיים משמשים בהתאם לצורך ולזמינות הנתונים. בדוגמא הקודמת, הפירמה הייתה פירמה ציבורית, מה שאומר שמחירי מניותיה מצוטטים בשוק פעיל ושסטיית התקן ההונית (קרי, התנודתיות של תשואות מניות הפירמה) המשתמעת באופן ישיר או עקיף מנתוני שוק הנצפים באופן ישיר או עקיף. בדוגמא הבאה, אנו מניחים כי הפירמה הינה פירמה פרטית, מה שאומר שמחירי מניותיה אינם מצוטטים בשוק פעיל ושסטיית התקן ההונית הינה תוצאת חישובי מודלים שונים, המשתמעים וניתנים ליישום באופן ישיר או עקיף חלף נתוני שוק הנצפים באופן ישיר או עקיף. בדוגמא זו נחשב את ההסתברות לחדלות פירעון או את נקודת חדלות הפירעון עבור החברה כאשר התחייבויותיה עולות על נכסיה, בהתחשב בשיעורי הצמיחה של נכסיה ובסטיית התקן הנכסית (קרי, התנודתיות של תשואות נכסי הפירמה) על פני זמן (תרשים 3). נציין כי בטרם השימוש במודל זה מומלץ להשתמש תחילה במודל השוק החיצוני עבור חברה ציבורית. נציין כי קיימות הקבלות מתודולוגיות דומות בין שני המודלים הללו, כאשר דוגמא זו בנויה על הבנת הדוגמא הקודמת כמובן.
תרשים 3 ההסתברות לחדלות פירעון של חברה פרטית
בתרשים 3, לפירמה שלה נכסים בערך פנקסני של 12 מיליון ₪, חוב בעלות פנקסנית של 10 מיליון ₪ ושיעורי צמיחה משמעותיים של נכסיה הפנימיים וסטיית תקן נכסית נמוכה– ישנה הסתברות לחדלות פירעון של 0.67%. בנוסף, במקום להסתמך על הערכת שווי הפירמה, ניתן להשתמש באמות מידה השוואתיות (benchmarks) מהשוק החיצוני, ככל ונתונים שכאלה זמינים.
בתרשים 4, ניתן להיווכח כי תשומות נוספות כגון תנודות השוק (תשואות השוק וסטיית התקן של השוק) והקורלציה (המתאם האמפירי בין רמת הסיכון של נכסי החברה לבין רמת הסיכון של השוק) נדרשות אף הן לצורך החישוב.
תרשים 4 ההסתברות לחדלות פירעון של יישות פרטית מכויילת לתנודות השוק
*סדרת מאמרים זו נכתבה על ידי הכותבים בהתבסס על ניסיונו האינטנסיבי של מר פולניצר בתחום הערכות השווי והאקטואריה הפיננסית, הכולל ביצוע, פיקוח וניהול של מאות הערכות שווי ועבודות אקטואריה פיננסית עבור משרדי רואי חשבון, משרדי ייעוץ כלכלי, חברות ציבוריות ופרטיות, כמו גם על מחקרים אמפיריים שפירסם כמאמרים אקדמיים בכתבי עת מקצועיים שפיטים ועל עשרות מאמרים מקצועיים בנושא הערכות שווי ואקטואריה פיננסית שפורסמו באתרי אינטרנט שונים. סדרת מאמרים זו משתמשת בפתרונות ממוחשבים מבוססי אקסל שפיתח מר פולניצר.
רועי פולניצר הינו בעליו של משרד הייעוץ הכלכלי "שווי פנימי – מעריכי שווי בלתי תלויים". מר פולניצר הינו בעל ניסיון רב בתחום הערכות השווי והאקטואריה הפיננסית, בין היתר, כמנהל סיכונים ומודליסט ראשי של ועדת השקעות באוניברסיטת בן גוריון, מנהל סיכונים וראש תחום שווי הוגן של חברת עגן יעוץ אקטוארי פיננסי ועסקי בע"מ, ראש תחום הערכות השווי במשרד רואי חשבון רווה–רביד (Russell Bedford ישראל) וכעוזר מחקר בתחום ניהול הסיכונים בבנקאות הישראלית של ה"ה ד"ר שילה ליפשיץ ז"ל.
מר פולניצר הינו מוסמך כמעריך שווי מימון תאגידי (CFV), כמעריך שווי מימון כמותי (QFV), כמודליסט פיננסי וכלכלי (FEM), אקטואר סיכוני שוק (MRA), כאקטואר סיכוני אשראי (CRA), כאקטואר סיכונים תפעוליים (ORA), כאקטואר סיכוני השקעות (IRA), כאקטואר סיכוני חיים (LRA) וכאקטואר סיכונים פנסיוניים (PRA) מטעם לשכת מעריכי השווי והאקטוארים הפיננסיים בישראל (IAVFA) ומשמש גם כיו"ר ומנכ"ל הלשכה. כמו כן, מר פולניצר הינו מוסמך כמנהל סיכונים פיננסיים (FRM) מטעם האיגוד העולמי למומחי סיכונים (GARP) וכמנהל סיכונים מוסמך (CRM) על ידי האיגוד הישראלי למנהלי סיכונים (IARM), בעל תואר B.A בכלכלה ו- M.B.A במנהל עסקים עם התמחות במימון מאוניברסיטת בן גוריון ושימש כעוזר הוראה של ה"ה ד"ר שילה ליפשיץ ז"ל בקורסים במימון ובנקאות במוסדות אקדמיים שונים, מרצה בקורסים בנגזרות וניהול סיכונים במכללה האקדמית אחווה, מרצה בקורסים בניתוח דוחות כספיים והערכת שווי במכללה האקדמית אשקלון וכמרצה בקורסים בניתוח ניירות ערך, מכשירים פיננסיים וניהול תיקים בקורס הכנה פרטי לבחינות הרשות לניירות ערך לרישיון מנהל תיקים בישראל.
נועם בלזברג – בעליו של משרד הייעוץ הכלכלי קופולה. מר בלזברג הינו בעליו של משרד הייעוץ הכלכלי "קופולה ניהול סיכונים". מר בלזברג הינו בעל ניסיון רב בתחום האשראי והאקטואריה הפיננסית, בין היתר, כקצין האשראי הראשי בבנק HSBC סניף ישראל, מנהל סיכונים ראשי ומנהל פרויקט באזל בבנק דקסיה ישראל, ראש צוות ניתוח פרויקטים ותוכניות השקעה בבנק לאומי וכראש צוות אשראי באגף הנדל"ן והתשתיות בבנק דיסקונט.
מר בלזברג הינו מוסמך כמעריך שווי מימון כמותי (QFV), כאקטואר סיכוני שוק (MRA), כאקטואר סיכוני אשראי (CRA), כאקטואר סיכונים תפעוליים (ORA) וכאקטואר סיכוני השקעות (IRA) מטעם לשכת מעריכי השווי והאקטוארים הפיננסיים בישראל (IAVFA) ונמנה על מייסדיה. כמו כן, מר בלזברג הינו מוסמך כמנהל סיכונים פיננסיים (FRM) מטעם האיגוד העולמי למומחי סיכונים (GARP), בעל רישיון שמאי מקרקעין בישראל מטעם מועצת שמאי המקרקעין, תארי B.A בכלכלה וניהול מאוניברסיטת בן גוריון ו- M.A בכלכלה מאוניברסיטת תל אביב ודיפולומה בשמאות ובניהול מקרקעין מאוניברסיטת תל אביב ומשמש מזה שנים רבות כסגן יו"ר הסניף האקדמי של GARP ישראל וכמנהל המקצועי של קורס ניהול סיכונים פיננסיים – הכנה לבחינות ה- FRM, בקמפוס לימודי החוץ של אוניברסיטת אריאל ברמת-אביב.
Tags: אקטואריה הערכת שווי כלכלה פיננסים תשואה